Glasnik Matematicki, Vol. 50, No. 2 (2015), 429-440.
LOCALIZED SVEP AND THE COMPONENTS OF QUASI-FREDHOLM RESOLVENT SET
Qingping Zeng, Huaijie Zhong and Qiaofen Jiang
College of Computer and Information Sciences, Fujian Agriculture and Forestry University, 350002 Fuzhou, P.R. China
e-mail: zqpping2003@163.com
School of Mathematics and Computer Science, Fujian Normal University, 350007 Fuzhou, P.R. China
e-mail: zhonghuaijie@sina.com
e-mail: bj001_ren@163.com
Abstract.
In this paper, new characterizations of the single valued extension property are given,
for a bounded linear operator T acting on a Banach space and its adjoint T*,
at Λ0 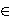 C in the case that Λ0 I - T is
quasi-Fredholm. With the help of a classical perturbation result
concerning operators with eventual topological uniform descent, we show the constancy of
certain subspace valued mappings on the components of quasi-Fredholm resolvent set.
As a consequence, we obtain a classification of these components.
C in the case that Λ0 I - T is
quasi-Fredholm. With the help of a classical perturbation result
concerning operators with eventual topological uniform descent, we show the constancy of
certain subspace valued mappings on the components of quasi-Fredholm resolvent set.
As a consequence, we obtain a classification of these components.
2010 Mathematics Subject Classification.
47A10, 47A11, 47A55.
Key words and phrases. Single valued extension property, quasi-Fredholm operators, quasi-Fredholm resolvent set.
Full text (PDF) (free access)
DOI: 10.3336/gm.50.2.11
References:
- P. Aiena, Fredholm and local spectral theory, with application to multipliers,
Kluwer Academic Publishers, Dordrecht, 2004.
MathSciNet
- P. Aiena, Quasi-Fredholm operators and localized SVEP,
Acta Sci. Math. (Szeged) 73 (2007), 251-263.
MathSciNet
- P. Aiena and F. Villafañe, Components of resolvent sets and local spectral
theory, Contemp. Math. 328 (2003), 1-14.
MathSciNet
CrossRef
- M. Berkani, Restriction of an operator to the range of its powers,
Studia Math. 140 (2000), 163-175.
MathSciNet
- M. Burgos, A. Kaidi, M. Mbekhta and M. Oudghiri, The descent
spectrum and perturbations, J. Operator Theory 56 (2006), 259-271.
MathSciNet
- N. Dunford, Spectral theory II. Resolutions of the identity, Pacific J. Math. 2 (1952), 559-614.
MathSciNet
CrossRef
- N. Dunford, Spectral operators, Pacific J. Math. 4 (1954), 321-354.
MathSciNet
CrossRef
- J. Finch, The single valued extension property on a banach space, Pacific J. Math. 58 (1975), 61-69.
MathSciNet
CrossRef
- S. Grabiner, Uniform ascent and descent of bounded operators, J. Math. Soc. Japan 34 (1982), 317-337.
MathSciNet
CrossRef
- M. A. Kaashoek, Ascent, descent, nullity and defect, a note on a paper by A. E. Taylor, Math. Ann. 172 (1967), 105-115.
MathSciNet
CrossRef
- T. Kato, Perturbation theory for nullity, deficiency and other quantities of linear operators, J. Analyse Math. 6 (1958), 261-322.
MathSciNet
CrossRef
- T. Kato, Perturbation theory for linear operators, Spring-verlag, Berlin-Heidelberg-New York-Tokyo, 1995.
MathSciNet
- J.-P. Labrousse, Les opérateurs quasi Fredholm: une généralisation des opérateurs semi Fredholm, Rend. Circ. Mat. Palermo (2) 29 (1980), 161-258.
MathSciNet
CrossRef
- K. B. Laursen and M. M. Neumann, An introduction to local spectral theory, Oxford University Press, New York, 2000.
MathSciNet
- M. Mbekhta and V. Müller, On the axiomatic theory of spectrum. II, Studia Math. 119 (1996), 129-147.
MathSciNet
- M. Mbekhta and A. Ouahab, Perturbation des opérateurs s-réguliers, in Topics in operator theory, operator algebras and applications,
Timisoara, 1994, Rom. Acad. Bucharest, 1995, 239-249.
MathSciNet
- V. Müller, On the regular spectrum, J. Operator Theory 31 (1994), 363-380.
MathSciNet
- V. Müller, On the Kato-decomposition of quasi-Fredholm and B-Fredholm operators, Vienna, Preprint ESI 1013, 2001.
Glasnik Matematicki Home Page
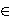 C in the case that Λ0 I - T is
quasi-Fredholm. With the help of a classical perturbation result
concerning operators with eventual topological uniform descent, we show the constancy of
certain subspace valued mappings on the components of quasi-Fredholm resolvent set.
As a consequence, we obtain a classification of these components.
C in the case that Λ0 I - T is
quasi-Fredholm. With the help of a classical perturbation result
concerning operators with eventual topological uniform descent, we show the constancy of
certain subspace valued mappings on the components of quasi-Fredholm resolvent set.
As a consequence, we obtain a classification of these components.