Glasnik Matematicki, Vol. 50, No. 2 (2015), 363-371.
ON CERTAIN IDENTITY RELATED TO JORDAN *-DERIVATIONS
Irena Kosi-Ulbl and Joso Vukman
Faculty of Mechanical Engineering,
University of Maribor,
Smetanova 17, 2000 Maribor,
Slovenia
e-mail: irena.kosi@um.si
Koroška cesta 57, 2000 Maribor,
Slovenia
e-mail: joso.vukman@guest.um.si
Abstract.
In this paper we prove the following result. Let H be a
real or complex Hilbert space, let L(H) be the algebra of all bounded linear operators on H and
let A(H) ⊆
L(H) be a standard operator algebra. Suppose we have an additive mapping
D:A(H) → L(H) satisfying the relation D(An)=D(A)A* n-1+AD(An-2)A*
+An-1D(A) for all A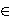 A(H) and some fixed integer n>1. In this case
there exists a unique B
A(H) and some fixed integer n>1. In this case
there exists a unique B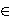 L(H) such that D(A)=BA*-AB holds for all A
L(H) such that D(A)=BA*-AB holds for all A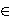 A(H).
A(H).
2010 Mathematics Subject Classification.
16W10, 46K15, 39B05.
Key words and phrases. Ring, ring with involution, prime ring,
semiprime ring, Hilbert space, standard operator algebra, *-derivation, Jordan *-derivation.
Full text (PDF) (free access)
DOI: 10.3336/gm.50.2.07
References:
- M. Brešar and J. Vukman, On some additive mappings in
rings with involution, Aequationes Math. 38 (1989), 178-185.
MathSciNet
CrossRef
- M. Brešar and B. Zalar, On the structure of Jordan
*-derivations, Colloq. Math. 63 (1997), 163-171.
MathSciNet
- H. G. Dales, Automatic continuity: a survey, Bull. Lond. Math. Soc.
10 (1978), 129-183.
MathSciNet
CrossRef
- M. G. Dales, Banach algebras and automatic continuity,
Calderon Press, Oxford, 2001.
MathSciNet
- D. Ilišević, Equations arising from Jordan
*-derivation pairs, Aequationes Math. 67 (2004), 236-240.
MathSciNet
CrossRef
- D. Ilišević, On quadratic functionals from
*-rings to a class of Banach *-algebras, in Proceedings of the
Postgraduate School and Conference Functional Analysis VIII, Aarhus Univ., Aarhus, 2004, 110-115.
MathSciNet
- D. Ilišević, Quadratic functionals on modules
over *-rings, Studia Sci. Math. Hungar. 42 (2005), 95-105.
MathSciNet
CrossRef
- D. Ilišević, Quadratic functionals on modules
over alternative *-rings, Studia Sci. Math. Hungar. 42 (2005), 459-469.
MathSciNet
CrossRef
- S. Kurepa, The Cauchy functional equation and scalar
product in vector spaces, Glasnik Mat. Fiz.-Astronom. Ser. II Društvo Mat. Fiz. Hrvatske 19 (1964), 23-26.
MathSciNet
- S. Kurepa, Quadratic and sesquilinear functionals,
Glasnik Mat. Fiz.-Astronom. Ser. II Društvo Mat. Fiz. Hrvatske 20 (1965), 79-92.
MathSciNet
- L. Molnár, Jordan *-derivation pairs on a
complex *-algebras, Aequationes Math. 54 (1997), 44-55.
MathSciNet
CrossRef
- A. M. Sinclair, Automatic continuity of linear
operators, Cambridge University
Press, Cambridge, London, New York and Melbourne, 1976.
MathSciNet
CrossRef
- P. Šemrl, On quadratic functionals, Bull. Aust.
Math. Soc. 37 (1988), 27-28.
MathSciNet
CrossRef
- P. Šemrl, Quadratic and quasi-quadratic functionals,
Proc. Amer. Math. Soc. 119 (1993), 1105-1113.
MathSciNet
CrossRef
- P. Šemrl, Jordan *-derivations of standard
operator algebras, Proc. Amer. Math. Soc. 120 (1994), 515-518.
MathSciNet
CrossRef
- P. Vrbová, Quadratic functionals and bilinear forms,
Časopis Pest. Mat. 98 (1973), 159-161.
MathSciNet
- J. Vukman, A result concerning additive functions in
hermitian Banach *-algebras and an application, Proc. Amer. Math.
Soc. 91 (1984), 367-372.
MathSciNet
CrossRef
- J. Vukman, Some results concerning the Cauchy
functional equation in certain Banach algebras, Bull. Aust. Math. Soc.
31 (1985), 137-144.
MathSciNet
CrossRef
- J. Vukman, Some functional equations in Banach algebras
and an application, Proc. Amer. Math. Soc. 100 (1987), 133-136.
MathSciNet
CrossRef
- J. Vukman, A note on Jordan *-derivations in
semiprime rings with involution, Int. Math. Forum 1 (2006), 617-622.
MathSciNet
- D. Yang, Jordan *-derivation pairs on standard
operator algebras and related results, Colloq. Math. 102 (2005), 137-145.
MathSciNet
CrossRef
- B. Zalar, Jordan-von Neumann theorem for Saworotnow's
generalized Hilbert space, Acta Math. Hungar. 69 (1995), 301-325.
MathSciNet
CrossRef
- B. Zalar, Jordan *-derivation pairs and
quadratic functionals on modules over *-rings, Aequationes Math.
54 (1997), 31-43.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
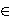 A(H) and some fixed integer n>1. In this case
there exists a unique B
A(H) and some fixed integer n>1. In this case
there exists a unique B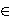 L(H) such that D(A)=BA*-AB holds for all A
L(H) such that D(A)=BA*-AB holds for all A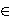 A(H).
A(H).
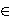 A(H) and some fixed integer n>1. In this case
there exists a unique B
A(H) and some fixed integer n>1. In this case
there exists a unique B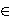 L(H) such that D(A)=BA*-AB holds for all A
L(H) such that D(A)=BA*-AB holds for all A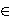 A(H).
A(H).