Glasnik Matematicki, Vol. 50, No. 2 (2015), 269-277.
ON TWO OF JOHN LEECH'S UNSOLVED PROBLEMS CONCERNING RATIONAL CUBOIDS
Allan MacLeod
Statistics, O.R. and Mathematics Group,
University of the West of Scotland, High St., Paisley,, Scotland. PA1 2BE
e-mail: allan.macleod@uws.ac.uk
Abstract.
Let {X,Y,Z,A,B,C} 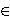 ℚ+ be such that X2+Y2=A2, X2+Z2=B2 and Y2+Z2=C2.
We consider the problem of finding T
ℚ+ be such that X2+Y2=A2, X2+Z2=B2 and Y2+Z2=C2.
We consider the problem of finding T 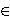 ℚ+ such that either
ℚ+ such that either
T2-X2=◻, T2-Y2=◻, T2-Z2=◻
or
T2-A2=◻, T2-B2=◻, T2-C2=◻.
We show that problem 2 always has a solution and we provide a formula for T. Extensive
computation has been unable to find a single solution of problem 1.
2010 Mathematics Subject Classification.
11D09, 11Y50.
Key words and phrases. Rational cuboid, elliptic curve.
Full text (PDF) (free access)
DOI: 10.3336/gm.50.2.02
References:
- A. Bremner, The rational cuboid and a quartic
surface, Rocky Mountain J. Math. 18 (1988), 105-121.
MathSciNet
CrossRef
- R. K. Guy, Unsolved problems in number theory,
3rd ed., Springer-Verlag, New York, 2004.
MathSciNet
CrossRef
- J. Leech, The rational cuboid revisited, Amer. Math. Monthly 84, (1977), 518-533.
MathSciNet
CrossRef
- R. van Luijk, On perfect cuboids, Undergraduate Thesis, Leiden University, 2000.
- L. J. Mordell, Diophantine equations, Academic
Press, London, 1969.
MathSciNet
- J. H. Silverman and J. Tate, Rational points on
elliptic curves, Springer-Verlag, New York, 1992.
MathSciNet
CrossRef
- D. Simon, Computing the rank of elliptic curves over number fields, LMS J. Comput. Math. 5 (2002), 7-17.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
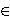 ℚ+ be such that X2+Y2=A2, X2+Z2=B2 and Y2+Z2=C2.
We consider the problem of finding T
ℚ+ be such that X2+Y2=A2, X2+Z2=B2 and Y2+Z2=C2.
We consider the problem of finding T 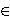 ℚ+ such that either
ℚ+ such that either
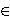 ℚ+ be such that X2+Y2=A2, X2+Z2=B2 and Y2+Z2=C2.
We consider the problem of finding T
ℚ+ be such that X2+Y2=A2, X2+Z2=B2 and Y2+Z2=C2.
We consider the problem of finding T 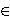 ℚ+ such that either
ℚ+ such that either