Glasnik Matematicki, Vol. 50, No. 1 (2015), 65-76.
RATIONAL FUNCTION VARIANT OF A PROBLEM OF ERDÖS AND GRAHAM
Szabolcs Tengely and Nóra Varga
Mathematical Institute,
University of Derecen,
P.O.Box 12, 4010 Debrecen,
Hungary
e-mail: tengely@science.unideb.hu
Institute of Mathematics, MTA-DE Research Group "Equations, Functions and Curves",
Hungarian Academy of Sciences and University of Debrecen,
P. O. Box 12, H-4010 Debrecen,
Hungary
e-mail: nvarga@science.unideb.hu
Abstract.
In this paper we provide bounds for the size of the solutions of the Diophantine equations
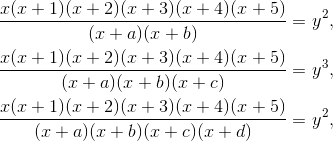
where a,b,c,d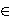 Z are pairwise distinct integers.
Z are pairwise distinct integers.
2010 Mathematics Subject Classification.
11D61, 11Y50.
Key words and phrases. Diophantine equations.
Full text (PDF) (free access)
DOI: 10.3336/gm.50.1.06
References:
-
M. Bauer and M. A. Bennett, Applications of the hypergeometric method to the generalized Ramanujan-Nagell equation, Ramanujan J. 6 (2002), 209-270.
MathSciNet
CrossRef
- M. A. Bennett, N. Bruin, K. Györy, and L. Hajdu, Powers from products of consecutive terms in arithmetic progression, Proc. London Math. Soc. 92 (2006), 273-306.
MathSciNet
CrossRef
-
M. A. Bennett and R. Van Luijk, Squares from blocks of consecutive integers: a problem of Erdös and Graham, Indag. Math., New Ser. 23 (2012), 123-127.
MathSciNet
CrossRef
-
L.E. Dickson, History of the theory of numbers. Vol II: Diophantine
analysis, Chelsea Publishing Co., New York, 1966.
MathSciNet
-
P. Erdös, Note on the product of consecutive integers (II), J. London Math. Soc. 14 (1939), 245-249.
MathSciNet
CrossRef
-
P. Erdös and R. L. Graham, Old and new problems and results in combinatorial number
theory, Monographies de L'Enseignement Mathématique, Geneva, 1980.
MathSciNet
-
P. Erdös and J. L. Selfridge The product of consecutive integers is never a power, Illinois J. Math. 19 (1975), 292-301.
MathSciNet
CrossRef
-
M. Fujiwara, Über die obere Schranke des absoluten Betrages der Wurzeln einer
algebraischen Gleichung, Tôhoku Math. J. 10 (1916), 167-171.
-
K. Györy, On the diophantine equation n(n+1) ... (n+k-1)=bxl ,
Acta Arith. 83 (1998), 87-92.
MathSciNet
-
K. Györy, L. Hajdu, and Á. Pintér, Perfect powers from products of consecutive terms in arithmetic progression, Compos. Math. 145 (2009), 845-864.
MathSciNet
CrossRef
-
K. Györy, L. Hajdu, and N. Saradha, On the Diophantine equation n(n+d)...(n+(k-1)d)=byl, Canad. Math. Bull. 47 (2004), 373-388.
MathSciNet
CrossRef
-
L. Hajdu, Sz. Tengely, and R. Tijdeman, Cubes in products of terms in arithmetic progression, Publ. Math. Debrecen 74 (2009), 215-232.
MathSciNet
-
N. Hirata-Kohno, S. Laishram, T. N. Shorey, and R. Tijdeman, An extension of a theorem of Euler, Acta Arith. 129 (2007), 71-102.
MathSciNet
CrossRef
-
S. Laishram and T. N. Shorey, The equation n(n+d)...(n+(k-1)d)=by2 with ω(d)≤ 6
or d≤ 1010, Acta Arith. 129 (2007), 249-305.
MathSciNet
CrossRef
-
F. Luca and P.G. Walsh, On a diophantine equation related to a conjecture of Erdös and Graham, Glas. Mat. Ser. III 42 (2007), 281-289.
MathSciNet
CrossRef
-
R. Obláth, Über das Produkt fünf aufeinander folgender Zahlen in einer
arithmetischen Reihe, Publ. Math. Debrecen 1 (1950), 222-226.
MathSciNet
-
O. Rigge, Über ein diophantisches problem, in: 9th Congress Math. Scand., Helsingfors 1938., 155-160.
-
A. Sankaranarayanan and N. Saradha, Estimates for the solutions of certain Diophantine equations by Runge's method,
Int. J. Number Theory 4 (2008), 475-493.
MathSciNet
CrossRef
-
N. Saradha, On perfect powers in products with terms from arithmetic
progressions, Acta Arith. 82 (1997), 147-172.
MathSciNet
-
N. Saradha and T. N. Shorey, Almost squares in arithmetic progression, Compositio Math. 138 (2003), 73-111.
MathSciNet
CrossRef
-
M. Skałba, Products of disjoint blocks of consecutive integers which are
powers, Colloq. Math. 98 (2003), 1-3.
MathSciNet
CrossRef
-
W. A. Stein et al., Sage Mathematics Software (Version 6.0),
The Sage Development Team, 2014, http://www.sagemath.org.
-
Sz. Tengely, Note on the paper: "An extension of a theorem of Euler" [Acta
Arith. 129 (2007), 71-102; MR2326488] by N. Hirata-Kohno,
S. Laishram, T. N. Shorey and R. Tijdeman.
Acta Arith. 134 (2008), 329-335.
MathSciNet
CrossRef
-
Sz. Tengely and N. Varga, On a generalization of a problem of Erdös and Graham, Publ. Math. Debrecen 84 (2014), 475-482.
CrossRef
-
M. Ulas, On products of disjoint blocks of consecutive integers,
Enseign. Math. (2) 51 (2005), 331-334.
MathSciNet
Glasnik Matematicki Home Page
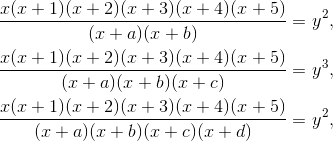
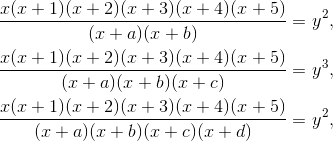
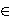 Z are pairwise distinct integers.
Z are pairwise distinct integers.