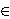 G-A such that for all h
G-A such that for all h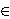 A we have either hv=h-1 or hv=h -1+2e-1.
A we have either hv=h-1 or hv=h -1+2e-1.
Abstract.
We determine up to isomorphism finite non-Dedekindian p-groups G (i.e., p-groups which possess non-normal subgroups) such that the normal closure
of each non-normal cyclic subgroup in G is nonabelian. It turns out that we must have p=2 and G has an abelian maximal subgroup A
of exponent 2e, e≥ 3, and an element v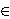 G-A such that for all h
G-A such that for all h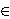 A we have either hv=h-1 or hv=h -1+2e-1.
A we have either hv=h-1 or hv=h -1+2e-1.
2010 Mathematics Subject Classification. 20D15.
Key words and phrases. Finite p-groups, normal closure, quasidihedral 2-groups, quasi-generalized quaternion groups, exponent of a p-group.
DOI: 10.3336/gm.49.2.07
References:
MathSciNet
MathSciNet