Glasnik Matematicki, Vol. 49, No. 2 (2014), 287-302.
SOME EXPERIMENTS WITH RAMANUJAN-NAGELL TYPE DIOPHANTINE EQUATIONS
Maciej Ulas
Jagiellonian University, Faculty of Mathematics and Computer Science, Institute of Mathematics, Łojasiewicza 6, 30 - 348 Kraków,
Poland
e-mail: maciej.ulas@uj.edu.pl
Abstract.
Stiller proved that the Diophantine equation x2+119=15 · 2n has exactly six solutions in positive integers. Motivated by this result we are interested in constructions of Diophantine equations of Ramanujan-Nagell type x2=Akn+B with many solutions. Here, A,B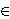 ℤ (thus A, B are not necessarily positive) and k
ℤ (thus A, B are not necessarily positive) and k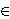 ℤ ≥ 2 are given integers. In particular, we prove that for each k there exists an infinite set S containing pairs of integers (A, B) such that for each (A,B)
ℤ ≥ 2 are given integers. In particular, we prove that for each k there exists an infinite set S containing pairs of integers (A, B) such that for each (A,B)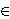 S we have gcd(A,B) is square-free and the Diophantine equation x2=Akn+B has at least four solutions in positive integers. Moreover, we construct several Diophantine equations of the form x2=Akn+B with k>2, each containing five solutions in non-negative integers.
We also find new examples of equations x2=A2n+B having six solutions in positive integers, e.g. the following Diophantine equations have exactly six solutions:
S we have gcd(A,B) is square-free and the Diophantine equation x2=Akn+B has at least four solutions in positive integers. Moreover, we construct several Diophantine equations of the form x2=Akn+B with k>2, each containing five solutions in non-negative integers.
We also find new examples of equations x2=A2n+B having six solutions in positive integers, e.g. the following Diophantine equations have exactly six solutions:
x2= 57· 2n+117440512, n=0 , 14 , 16, 20, 24, 25,
x2= 165· 2n+26404, n=0 , 5 , 7, 8, 10, 12.
Moreover, based on an extensive numerical calculations we state several conjectures on the number of solutions of certain parametric families of the Diophantine equations of Ramanujan-Nagell type.
2010 Mathematics Subject Classification.
11D41.
Key words and phrases. Diophantine equation, Ramanujan-Nagell equation.
Full text (PDF) (free access)
DOI: 10.3336/gm.49.2.04
References:
- R. Apéry, Sur une équation diophantienne, C. R. Acad. Sci. Paris, Sér. A 251 (1960), 1451-1452.
MathSciNet
- M. Bauer and M. Bennett, Applications of the hypergeometric method to the generalized Ramanujan-Nagell equation. (English summary)
Ramanujan J. 6 (2002), 209-270.
MathSciNet
CrossRef
- F. Beukers, On the generalized Ramanujan-Nagell equation I, Acta Arith. 38 (1980/1981), 389-410.
MathSciNet
- F. Beukers, On the generalized Ramanujan-Nagell equation II, Acta Arith. 39 (1981), 113-123.
MathSciNet
- Y. Bugeaud and T. Shorey, On the number of solutions of the generalized Ramanujan-Nagell equation, J. Reine Angew. Math. 539 (2001), 55-74.
MathSciNet
CrossRef
- W. Bosma, J. Cannon, and C. Playoust, The Magma algebra system.
I. The user language, J. Symbolic Comput., 24 (3-4) (1997), 235-265.
MathSciNet
CrossRef
- P. Bundschuh, On the diophantine equation of Ramanujan-Nagell, Semin. Math. Sci. 12 (1988), 31-40.
MathSciNet
- A. Dabrowski and M. Ulas, Variations on Brocard-Ramanujan equation, J. Number Theory 133 (2013), 1168-1185.
MathSciNet
CrossRef
- G. Faltings, Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Invent. Math. 73 (1983), 349-366.
MathSciNet
CrossRef
- H. Hasse, Über eine Diophantische Gleichung von Ramanujan-Nagell und ihre Verallgemeinerung, Nagoya Math. J. 27 (1966), 77-102.
MathSciNet
CrossRef
- T. Nagell, The Diophantine equation x2+7=2n, Ark. Math. 4 (1961), 185-187.
MathSciNet
CrossRef
- N. Saradha and A. Srinivasan, Generalized Lebesgue-Ramanujan-Nagell equations, Diophantine equations, 207-223, Tata Inst. Fund. Res., Mumbai, 2008.
MathSciNet
- J. Stiller, The Diophantine equation x2+119=15· 2n has exactly six solutions, Rocky Mountain J. Math. 26 (1) (1996), 295-298.
MathSciNet
CrossRef
- N. Tzanakis, On the Diophantine equation y2-D=2k, J. Number Theory 17 (1983), 144-164.
MathSciNet
CrossRef
- M. Ulas, Some observations on the Diophantine equation y2 = x! + A and related results, Bull. Aust. Math. Soc. 86 (2012), 377-388.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
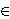 ℤ (thus A, B are not necessarily positive) and k
ℤ (thus A, B are not necessarily positive) and k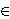 ℤ ≥ 2 are given integers. In particular, we prove that for each k there exists an infinite set S containing pairs of integers (A, B) such that for each (A,B)
ℤ ≥ 2 are given integers. In particular, we prove that for each k there exists an infinite set S containing pairs of integers (A, B) such that for each (A,B)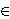 S we have gcd(A,B) is square-free and the Diophantine equation x2=Akn+B has at least four solutions in positive integers. Moreover, we construct several Diophantine equations of the form x2=Akn+B with k>2, each containing five solutions in non-negative integers.
We also find new examples of equations x2=A2n+B having six solutions in positive integers, e.g. the following Diophantine equations have exactly six solutions:
S we have gcd(A,B) is square-free and the Diophantine equation x2=Akn+B has at least four solutions in positive integers. Moreover, we construct several Diophantine equations of the form x2=Akn+B with k>2, each containing five solutions in non-negative integers.
We also find new examples of equations x2=A2n+B having six solutions in positive integers, e.g. the following Diophantine equations have exactly six solutions: