Glasnik Matematicki, Vol. 49, No. 1 (2014), 83-103.
FINITE GROUPS WITH FEW VANISHING ELEMENTS
Jinshan Zhang, Zhencai Shen and Jiangtao Shi
School of Science, Sichuan University of
Science and Engineering, 643000 Zigong, P. R. China
e-mail: zjscdut@163.com
College of Science, China Agricultural University, 100083 Beijing, P. R. China
e-mail: zhencai688@sina.com
School of Mathematics and Information Science, Yantai
University, 264005 Yantai, P. R. China
e-mail: shijt@math.pku.edu.cn
Abstract.
Let G be a finite group, and Irr(G) the set of
irreducible complex characters of G. We say that an element g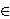 G is a vanishing element of G if there exists χ in
Irr(G) such that χ(g)= 0. Let Van(G) denote the set of
vanishing elements of G, that is, Van(G)= {g
G is a vanishing element of G if there exists χ in
Irr(G) such that χ(g)= 0. Let Van(G) denote the set of
vanishing elements of G, that is, Van(G)= {g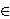 G|χ(g)=0
for some χ
G|χ(g)=0
for some χ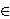 Irr (G)}. In this paper, we investigate the
finite groups G with the following property: Van(G) contains at
most four conjugacy classes of G.
Irr (G)}. In this paper, we investigate the
finite groups G with the following property: Van(G) contains at
most four conjugacy classes of G.
2010 Mathematics Subject Classification.
20C15.
Key words and phrases. Finite groups, characters, vanishing elements.
Full text (PDF) (free access)
DOI: 10.3336/gm.49.1.07
References:
- D. Bubboloni, S. Dolfi and P. Spiga,
Finite groups whose
irreducible characters vanish only on p-elements,
J. Pure Appl. Algebra 213 (2009), 370-376.
MathSciNet
CrossRef
- J. H. Conway, R. T. Curtis, S. P. Norton, R. A. Parker and R. A. Wilson, Atlas of finite groups, Oxford University Press, Eynsham, 1985.
MathSciNet
- S. Dolfi, E. Pacifici, L. Sanus and P. Spiga,
On the orders of zeros of irreducible characters,
J. Algebra 321 (2009), 345-352.
MathSciNet
CrossRef
- S. Dolfi, E. Pacifici, L. Sanus and P. Spiga,
On the vanishing prime graph of solvable groups,
J. Group Theory 13 (2010), 189-206.
MathSciNet
CrossRef
- M. Herzog,
On finite simple groups of order divisible by three primes only,
J. Algebra 10 (1968), 383-388.
MathSciNet
CrossRef
- B. Huppert,
Character theory of finite groups, de Gruyter, Berlin, 1998.
MathSciNet
- B. Huppert,
Endliche gruppen, Vol. 1, Springer-Verlag, Berlin-New York, 1967.
MathSciNet
- I. M. Isaacs,
Character theory of finite groups, Academic Prees, New York-London 1976.
MathSciNet
- I. M. Isaacs, G. Navarro and T. R. Wolf,
Finite group elements where no irreducible character vanishes,
J. Algebra 222 (1999), 413-423.
MathSciNet
CrossRef
- G. James and M. Liebeck,
Representations and character of groups, Cambridge University Press, Cambridge, 1993.
MathSciNet
- O. Manz and T. R. Wolf,
Representations of solvable groups, Cambridge University Press, Cambridge, 1993.
MathSciNet
- V. D. Mazurov,
On groups that contain a self-centralizing subgroup of order 3,
Algebra and Logic 42 (2003), 29-36.
MathSciNet
CrossRef
- A. Moretó and J. Sangroniz,
On the number of conjugacy classes of zeros of characters,
Israel J. Math. 142 (2004), 163-187.
MathSciNet
CrossRef
- G. Qian,
Bounding the fitting height of a solvable
group by the number of zeros in a character table,
Proc. Amer. Math. Soc., 142 (2002), 3171-3176.
MathSciNet
CrossRef
- G. Qian, W. Shi and X. You,
Conjugacy classes outside a normal subgroup,
Comm. Algebra 32 (2004), 4809-4820.
MathSciNet
CrossRef
- Y. C. Ren, X. H. Liu and J. S. Zhang,
Notes on the restriction and the zeros of an irreducible character of a finite group,
Sichuan Daxue Xuebao 44 (2007),
1183-1188.
MathSciNet
- C. Shao, S. Humphries, X. You and J. Zhang,
A note on conjugacy classes outside a normal subgroup,
Comm. Algebra 37 (2009), 3306-3308.
MathSciNet
CrossRef
- A. Vera Lopez and J. Vera Lopez,
Classification of finite groups according to the number of conjugacy classes,
Israel J. Math. 51 (1985), 305-338.
MathSciNet
CrossRef
- W. J. Wong,
Finite groups with a self-centralizing subgroup of order 4,
J. Austral. Math. Soc. 7 (1967), 570-576.
MathSciNet
CrossRef
- J. S. Zhang, W. J. Shi and Z. C. Shen,
Finite groups in which every
irreducible character vanishes on at most three conjugacy classes,
J. Group Theory 13 (2010), 799-819.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
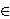 G is a vanishing element of G if there exists χ in
Irr(G) such that χ(g)= 0. Let Van(G) denote the set of
vanishing elements of G, that is, Van(G)= {g
G is a vanishing element of G if there exists χ in
Irr(G) such that χ(g)= 0. Let Van(G) denote the set of
vanishing elements of G, that is, Van(G)= {g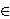 G|χ(g)=0
for some χ
G|χ(g)=0
for some χ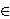 Irr (G)}. In this paper, we investigate the
finite groups G with the following property: Van(G) contains at
most four conjugacy classes of G.
Irr (G)}. In this paper, we investigate the
finite groups G with the following property: Van(G) contains at
most four conjugacy classes of G.