Glasnik Matematicki, Vol. 49, No. 1 (2014), 1-12.
THE EDGE WIENER INDEX OF SUSPENSIONS, BOTTLENECKS, AND THORNY GRAPHS
Yaser Alizadeh, Ali Iranmanesh, Tomislav Došlić and Mahdieh Azari
Department of Mathematics, Hakim Sabzevari University, Sabzevar, Iran
e-mail: y.alizadeh@hsu.ac.ir
Department of Mathematics, Tarbiat
Modares University, P. O. Box: 14115-137, Tehran, Iran
e-mail: iranmanesh@modares.ac.ir
Faculty of Civil Engineering, University of Zagreb, Kačićeva 26, 10000 Zagreb, Croatia
e-mail: doslic@grad.hr
Department of Mathematics, Kazerun Branch, Islamic Azad University, P. O. Box: 73135-168, Kazerun, Iran
e-mail: azari@kau.ac.ir
Abstract.
Let G be a simple connected graph. The distance
between the edges g and f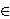 E(G) is defined as the distance
between the corresponding vertices g and f in the line graph
of G. The edge-Wiener index of G is defined as the sum of such
distances between all pairs of edges of the graph. Let G1+G2
and G1ο G2 be the join and the corona of graphs G1 and
G2, respectively. In this paper, we present explicit formulas
for the edge-Wiener index for these graphs. Then we apply our
results to compute the edge-Wiener index of suspensions,
bottlenecks, and thorny graphs.
E(G) is defined as the distance
between the corresponding vertices g and f in the line graph
of G. The edge-Wiener index of G is defined as the sum of such
distances between all pairs of edges of the graph. Let G1+G2
and G1ο G2 be the join and the corona of graphs G1 and
G2, respectively. In this paper, we present explicit formulas
for the edge-Wiener index for these graphs. Then we apply our
results to compute the edge-Wiener index of suspensions,
bottlenecks, and thorny graphs.
2010 Mathematics Subject Classification.
05C12, 05C76, 92E10.
Key words and phrases. Distance, edge-Wiener index, join, corona.
Full text (PDF) (free access)
DOI: 10.3336/gm.49.1.01
References:
-
M. Azari and A. Iranmanesh,
Computation of the edge Wiener indices of the sum of graphs,
Ars Combin. 100 (2011), 113-128.
MathSciNet
-
M. Azari, A. Iranmanesh and A. Tehranian, A method for calculating
an edge version of the Wiener number of a graph operation, Util. Math. 87 (2012), 151-164.
MathSciNet
-
M. Azari, A. Iranmanesh and A. Tehranian, Computation of the first
edge Wiener index of a composition of graphs, Studia Univ.
Babes Bolyai Chem. 4 (2010), 183-196.
-
M. Azari, A. Iranmanesh and A. Tehranian, Maximum and minimum
polynomials of a composite graph, Austral. J. Basic Appl.
Sci. 5(9) (2011), 825-830.
-
M. Azari, A. Iranmanesh and A. Tehranian, Two topological indices
of three chemical structures, MATCH Commun. Math. Comput.
Chem. 69 (2013), 69-86.
MathSciNet
- P. Dankelmann, I. Gutman, S. Mukwembi and H. C. Swart, The edge Wiener index of a graph, Discrete Math. 309
(2009), 3452-3457.
MathSciNet
CrossRef
- I. Gutman, A new method for the calculation of the Wiener number of acyclic molecules, J. Mol. Struct. (Theochem) 285 (1993), 137-142.
CrossRef
- I. Gutman, Calculating the Wiener number: the Doyle-Graver method, J. Serb. Chem. Soc. 58 (1993), 745-750.
- I. Gutman and N. Trinajstić, Graph theory and molecular orbitals, Total π- electron energy of alternant hydrocarbons, Chem. Phys. Lett.
17 (1972), 535-538.
CrossRef
- I. Gutman, Y. N. Yeh, S. L. Lee and Y. L. Luo, Some recent results in the theory of the Wiener number, Indian J. Chem. 32A (1993), 651-661.
- A. Iranmanesh, I. Gutman, O. Khormali and A. Mahmiani, The edge versions of Wiener index, MATCH Commun. Math. Comput. Chem. 61 (2009), 663-672.
MathSciNet
- M. Juvan, B. Mohar, A. Graovac, S. Klavžar and J. Žerovnik, Fast computation of the Wiener index of fasciagraphs and rotagraphs, J. Chem. Inf. Comput. Sci. 35 (1995), 834-840.
CrossRef
- M. H. Khalifeh, H. Yousefi Azari, A. R. Ashrafi and S. G. Wagner, Some new results
on distance-based graph invariants, European J. Combin.
30 (2009), 1149-1163.
MathSciNet
CrossRef
-
D. J. Klein, T. Došlić and D. Bonchev, Vertex-weightings for
distance moments and thorny graphs, Discrete Appl. Math. 155
(2007), 2294-2302.
MathSciNet
CrossRef
- H. Liu and X. F. Pan, On the Wiener index of trees with fixed diameter, MATCH Commun. Math. Comput. Chem. 60 (2008), 85-94.
MathSciNet
- A. Miličević and N. Trinajstić, Combinatorial
enumeration in chemistry, in Chemical Modelling: Applications
and Theory,
RSC Publishing, Cambridge, 2006,
405-469.
- P. Senn, The computation of the distance matrix and the Wiener index for graphs of arbitrary complexity with weighted vertices and edges, Comput. Chem. 12 (1988), 219-227.
CrossRef
- D. Stevanović, Maximizing Wiener index of graphs with fixed maximum degree, MATCH Commun. Math. Comput. Chem. 60 (2008), 71-83.
MathSciNet
- S. G. Wagner, A class of trees and its Wiener index, Acta Appl. Math. 91 (2006), 119-132.
MathSciNet
CrossRef
- H. Wiener, Structural determination of paraffin boiling points, J. Am. Chem. Soc. 69 (1947), 17-20.
CrossRef
- Z. Yarahmadi, T. Došlić and A. R. Ashrafi,
The bipartite edge frustration of composite graphs, Discrete
Appl. Math. 158 (2010), 1551-1558.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
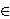 E(G) is defined as the distance
between the corresponding vertices g and f in the line graph
of G. The edge-Wiener index of G is defined as the sum of such
distances between all pairs of edges of the graph. Let G1+G2
and G1ο G2 be the join and the corona of graphs G1 and
G2, respectively. In this paper, we present explicit formulas
for the edge-Wiener index for these graphs. Then we apply our
results to compute the edge-Wiener index of suspensions,
bottlenecks, and thorny graphs.
E(G) is defined as the distance
between the corresponding vertices g and f in the line graph
of G. The edge-Wiener index of G is defined as the sum of such
distances between all pairs of edges of the graph. Let G1+G2
and G1ο G2 be the join and the corona of graphs G1 and
G2, respectively. In this paper, we present explicit formulas
for the edge-Wiener index for these graphs. Then we apply our
results to compute the edge-Wiener index of suspensions,
bottlenecks, and thorny graphs.