Glasnik Matematicki, Vol. 48, No. 2 (2013), 443-466.
SIMULTANEOUS Z/P-ACYCLIC RESOLUTIONS OF EXPANDING SEQUENCES
Leonard Rubin and Vera Tonić
Department of Mathematics,
University of Oklahoma,
601 Elm Ave, room 423,
Norman, Oklahoma 73019,
USA
e-mail: lrubin@ou.edu
Department of Mathematics,
Ben Gurion University of the Negev,
P.O.B. 653,
Be'er Sheva 84105,
Israel
e-mail: vera.tonic@gmail.com
Abstract. We prove the following theorem.
Theorem. Let
X be a nonempty compact metrizable space, let l1≤ l2≤ ⋅⋅⋅ be a sequence in N, and let X1 ⊂
X2⊂ ⋅⋅⋅ be a sequence of nonempty closed subspaces of X such
that for each k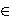 N, dimZ/p Xk≤ lk. Then there
exists a compact metrizable space Z, having closed subspaces
Z1⊂ Z2⊂ ⋅⋅⋅, and a (surjective) cell-like map
π:Z → X, such that for each k
N, dimZ/p Xk≤ lk. Then there
exists a compact metrizable space Z, having closed subspaces
Z1⊂ Z2⊂ ⋅⋅⋅, and a (surjective) cell-like map
π:Z → X, such that for each k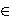 N,
N,
(a) dim Zk≤ lk,
(b) π(Zk)=Xk, and
(c) π|Zk:Zk→ Xk is a Z/p-acyclic map.
Moreover, there is a sequence A1⊂ A2⊂⋅⋅⋅ of
closed subspaces of Z such that for each k, dim Ak≤ lk,
π|Ak:Ak → X is surjective, and for k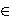 N,
Zk⊂ Ak and π|Ak:Ak→ X is a UVlk-1-map.
N,
Zk⊂ Ak and π|Ak:Ak→ X is a UVlk-1-map.
It is not required that X=∪∞k=1 Xk or that Z=∪∞k=1 Zk.
This result generalizes the Z/p-resolution theorem of A. Dranishnikov and runs parallel to a similar theorem
of S. Ageev, R. Jiménez, and the first author, who studied the situation where the group was
Z.
2010 Mathematics Subject Classification.
55M10, 54F45, 55P20.
Key words and phrases. Cell-like map, cohomological dimension, CW-complex, dimension, Edwards-Walsh resolution, Eilenberg-MacLane complex, G-acyclic map, inverse sequence, simplicial complex, UVk-map.
Full text (PDF) (free access)
DOI: 10.3336/gm.48.2.15
References:
- S. Ageev, R. Jiménez and L. Rubin, Cell-like resolutions in the strongly countable Z-dimensional case, Topology Appl. 140 (2004), 5-14.
MathSciNet
CrossRef
- R. Daverman,
Decompositions of Manifolds, Academic Press, Orlando, 1986.
MathSciNet
- A. N. Dranishnikov, Cohomological dimension theory of compact metric spaces, Topology Atlas Invited Contributions,
http://at.yorku.ca/t/a/i/c/43.pdf.
- J. Dydak and J. Walsh, Complexes that arise in cohomological dimension theory: a unified approach, J. London Math. Soc. (2) (48) (1993), 329-347.
MathSciNet
CrossRef
- R. D. Edwards, A theorem and a question related to cohomological dimension
and cell-like maps,
Notices Amer. Math. Soc. 25 (1978), A58-A59.
- L. C. Glaser, Geometrical combinatorial topology, Vol. I, Van Nostrand Math. Studies, 1970.
- W. Hurewicz and H. Wallman, Dimension theory, Princeton University Press, Princeton, 1941.
MathSciNet
- V. I. Kuz'minov, Homological dimension
theory, Russian Math. Surveys 23 (1968), 1-45.
MathSciNet
- A. Koyama and K. Yokoi, Cohomological dimension and acyclic resolutions, Topology Appl. 120 (2002), 175-204.
MathSciNet
CrossRef
- M. Levin, Acyclic resolutions for arbitrary groups, Isr. J. Math. 135 (2003), 193-203.
MathSciNet
CrossRef
- S. Mardešić and J. Segal, Shape theory,
North-Holland, Amsterdam, 1982.
MathSciNet
- E. H. Spanier, Algebraic topology, McGraw-Hill, New York, 1966.
MathSciNet
- J. Walsh, Dimension, cohomological dimension, and cell-like mappings, in Shape theory and geometric
topology, Springer, Berlin, 1981, 105-118.
MathSciNet
Glasnik Matematicki Home Page
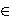 N, dimZ/p Xk≤ lk. Then there
exists a compact metrizable space Z, having closed subspaces
Z1⊂ Z2⊂ ⋅⋅⋅, and a (surjective) cell-like map
π:Z → X, such that for each k
N, dimZ/p Xk≤ lk. Then there
exists a compact metrizable space Z, having closed subspaces
Z1⊂ Z2⊂ ⋅⋅⋅, and a (surjective) cell-like map
π:Z → X, such that for each k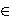 N,
N,
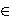 N,
Zk⊂ Ak and π|Ak:Ak→ X is a UVlk-1-map.
N,
Zk⊂ Ak and π|Ak:Ak→ X is a UVlk-1-map.