Glasnik Matematicki, Vol. 48, No. 1 (2013), 91-96.
COMMUTING AUTOMORPHISMS OF SOME FINITE GROUPS
S. Fouladi and R. Orfi
Faculty of Mathematical Sciences and Computer, Kharazmi University,
50 Taleghani Ave., Tehran 1561836314 , Iran
e-mail: s_fouladi@tmu.ac.ir
Department of Mathematics, Faculty of Science, Arak University, Arak 38156-8-8349, Iran
e-mail: r-orfi@araku.ac.ir
Abstract. Let G be a group. An automorphism α of G
is called a commuting automorphism if xxα=xα x for all x 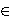 G. We denote the set of all commuting automorphisms of G by
A(G). Moreover a group G is called an AC-group if
the centralizer of every non-central element of G is abelian. In
this paper we show that A(G) is a subgroup of the
automorphism group of G for all finite AC-groups, p-groups
of maximal class, and metacyclic p-groups.
G. We denote the set of all commuting automorphisms of G by
A(G). Moreover a group G is called an AC-group if
the centralizer of every non-central element of G is abelian. In
this paper we show that A(G) is a subgroup of the
automorphism group of G for all finite AC-groups, p-groups
of maximal class, and metacyclic p-groups.
2010 Mathematics Subject Classification.
20F28, 20D15.
Key words and phrases. Commuting automorphisms, AC-groups, minimal
non-abelian p-groups, metacyclic p-groups,
p-groups of maximal class.
Full text (PDF) (free access)
DOI: 10.3336/gm.48.1.08
References:
- J. E. Adney and T. Yen, Automorphisms of a p-group, Illinois J.
Math. 9 (1965), 137-143.
MathSciNet
CrossRef
- H. E. Bell and W. S. Martindale,
Centralizing mappings of semiprime rings, Canad. Math.
Bull. 30 (1987), 92-101.
MathSciNet
CrossRef
- Y. Berkovich, Groups of prime power
order. Vol. 1, Walter de Gruyter, Berlin, 2008.
MathSciNet
CrossRef
- M. Deaconescu, G. Silberberg and G. L.
Walls, On commuting automorphisms of groups, Arch. Math. (Basel)
79 (2002), 423-429.
MathSciNet
CrossRef
- N. Divinsky, On commuting automorphisms
of rings, Trans. Roy. Soc. Canada. Sect. III. 49 (1955), 19-22.
MathSciNet
- B. Huppert, Endliche Gruppen. I,
Springer-Verlag, Berlin-New York, 1967.
MathSciNet
CrossRef
- D. L. Johnson, Presentation of groups, 2nd ed., Cambridge
University Press, Cambridge, 1997.
MathSciNet
CrossRef
- I. N. Herstein, J. L. Brenner and W. A. Newcomb, Problems and solutions: elementary problems: E3039-E3040,
Amer. Math. Monthly 91 (1984), 203.
MathSciNet
CrossRef
- I. N. Herstein, T. J. Laffey, and J. Thomas, Problems and solutions: solutions of elementary problems: E3039,
Amer. Math. Monthly 93 (1986), 816-817.
MathSciNet
CrossRef
- C. R. Leedham-Green and S. McKay, The
structure of groups of prime power order, Oxford University
Press, Oxford, 2002.
MathSciNet
- J. Luh, A note on commuting automorphisms
of rings, Amer. Math. Monthly 77 (1970), 61-62.
MathSciNet
CrossRef
- M. Pettet, Personal communication.
- P. Schmid, Normal p-subgroups in
the group of outer automorphisms of a finite p-group, Math.
Z. 147 (1976), 271-277.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
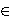 G. We denote the set of all commuting automorphisms of G by
A(G). Moreover a group G is called an AC-group if
the centralizer of every non-central element of G is abelian. In
this paper we show that A(G) is a subgroup of the
automorphism group of G for all finite AC-groups, p-groups
of maximal class, and metacyclic p-groups.
G. We denote the set of all commuting automorphisms of G by
A(G). Moreover a group G is called an AC-group if
the centralizer of every non-central element of G is abelian. In
this paper we show that A(G) is a subgroup of the
automorphism group of G for all finite AC-groups, p-groups
of maximal class, and metacyclic p-groups.