Glasnik Matematicki, Vol. 48, No. 1 (2013), 49-58.
SUMS OF BIQUADRATES AND ELLIPTIC CURVES
Julián Aguirre and Juan Carlos Peral
Departamento de Matemáticas,
Universidad del País Vasco UPV/EHU,
Aptdo. 644, 48080 Bilbao, Spain
e-mail: julian.aguirre@ehu.es
e-mail: juancarlos.peral@ehu.es
Abstract. Given the family of elliptic curves y2= x3-(1+u4) x, u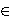 Q, or equivalently y2=x3-(m4+n4)x for m,n integers, we prove that its rank over Q(u) is 2.
We also show the existence of subfamilies of rank at least 3 and 4 over Q(u). Also, assuming the Parity Conjecture, we prove the existence of infinitely many curves having rank at least 5 over Q.
Q, or equivalently y2=x3-(m4+n4)x for m,n integers, we prove that its rank over Q(u) is 2.
We also show the existence of subfamilies of rank at least 3 and 4 over Q(u). Also, assuming the Parity Conjecture, we prove the existence of infinitely many curves having rank at least 5 over Q.
Performing an exhaustive search in the range 1 ≤ n < m ≤ 251000 we have found more than 1500 curves with rank 8, over 150 with rank 9, nine of rank 10 and one of rank 11. This improves previous results of Izadi, Khoshnam and Nabardi.
2010 Mathematics Subject Classification.
11G05.
Key words and phrases. Elliptic curve, rank, biquadrate.
Full text (PDF) (free access)
DOI: 10.3336/gm.48.1.04
References:
-
J. Aguirre, F. Castañeda and J. C. Peral, High rank elliptic curves with torsion group Z/(2 Z), Math. Comp. 73 (2004), 323-331
MathSciNet
CrossRef
-
J. Aguirre and J. C. Peral, Biquadrates and elliptic curves, preprint, http://arxiv.org/abs/1203.2576.
-
W. P. Barth, K. Hulek, C. A. M. Peters and A. Van de Ven, Compact complex surfaces, Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics 4, Springer-Verlag, Berlin, 2004.
MathSciNet
-
G. Campbell, Finding elliptic curves and families of elliptic curves over Q of
large rank, Thesis (Ph.D.)-Rutgers The State University of New Jersey - New
Brunswick, ProQuest LLC, Ann Arbor, MI, 1999.
MathSciNet
-
J. E. Cremona, Algorithms for modular elliptic curves, Cambridge University Press, Cambridge, 1997.
MathSciNet
-
L. E. Dickson, History of the theory of numbers. Vol. II: Diophantine analysis, Chelsea Publishing Co., New York, 1966.
MathSciNet
-
A. Dujella, High rank elliptic curves with prescribed torsion,
http://web.math.hr/ duje/tors/tors.html.
-
S. Fermigier, Construction of high-rank elliptic curves over Q and Q(t) with non-trivial 2-torsion (extended abstract), Algorithmic number theory, Talence, 1996., Lecture Notes in Comput. Sci. 1122, Springer, Berlin, 1996, 115-120.
MathSciNet
-
Y. Fujita and N. Terai, On the rank of the elliptic curve y2= x3- n x, Int. J. Algebra 6 (2012), 885-901.
MathSciNet
-
R. K. Guy, Unsolved problems in number theory, Springer-Verlag, New York, 2004.
MathSciNet
- G. H. Hardy and E. M. Wright, An introduction to the theory of numbers, Oxford University Press, Oxford, 2008.
MathSciNet
-
F. A. Izadi, F. Khoshnam and K. Nabardi, Sum of two biquadrates and elliptic curves of rank ≥ 4, preprint, http://arxiv.org/abs/1202.5676.
-
S. Kihara, On the rank of the elliptic curve y2=x3+kx, Proc. Japan Acad. Ser. A Math. Sci. 74 (1998), 115-116
MathSciNet
CrossRef
- S. Kihara, On the rank of the elliptic curve y2=x3+kx II, Proc. Japan Acad. Ser. A Math. Sci. 80 (2004), 24-25.
MathSciNet
CrossRef
- Wolfram Research, Mathematica Edition: Version 8.0, Champaign, Illinois, 2010.
-
R. Miranda, An overview of algebraic surfaces,
Algebraic geometry, Ankara, 1995. Lecture Notes in Pure and Appl. Math. 193, Dekker, New York, 1997, 157-217,
MathSciNet
-
K. Nagao, On the rank of elliptic curve y2=x3-kx, Kobe J. Math.,
11 (1994), 205-210.
MathSciNet
-
K. Ono and T. Ono,
Quadratic forms and elliptic curves. III,
Proc. Japan Acad. Ser. A Math. Sci. 72 (1996), 204-205.
MathSciNet
CrossRef
-
N. F. Rogers, Rank computations for the congruent number elliptic curves, Experiment. Math. 9 (2000), 591-594.
MathSciNet
CrossRef
-
T. Shioda, On the Mordell-Weil lattices,
Comment. Math. Univ. St. Paul. 39 (1990), 211-240.
MathSciNet
-
T. Shioda, Construction of elliptic curves with high rank via the invariants of the Weyl groups, J. Math. Soc. Japan 43 (1991), 673-719.
MathSciNet
CrossRef
- J. H. Silverman, Advanced topics in the arithmetic of elliptic curves, Graduate Texts in Mathematics 151, Springer-Verlag, New York, 1994.
MathSciNet
-
J. Steggall, The Equation x3-u3=y3-v3 when x,y,u,v are rational, Proc. Edinburgh Math. Soc. 34 (1915), 41-44.
CrossRef
-
J. Wroblewski, Equal Sums of Powers-Tables, http://www.math.uni.wroc.pl/ jwr/eslp/tables.htm
- A. J. Zajta, Solutions of the Diophantine equation
A4+B4=C4+D4, Math. Comp. 41 (1983), 635-659.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
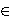 Q, or equivalently y2=x3-(m4+n4)x for m,n integers, we prove that its rank over Q(u) is 2.
We also show the existence of subfamilies of rank at least 3 and 4 over Q(u). Also, assuming the Parity Conjecture, we prove the existence of infinitely many curves having rank at least 5 over Q.
Q, or equivalently y2=x3-(m4+n4)x for m,n integers, we prove that its rank over Q(u) is 2.
We also show the existence of subfamilies of rank at least 3 and 4 over Q(u). Also, assuming the Parity Conjecture, we prove the existence of infinitely many curves having rank at least 5 over Q.