Glasnik Matematicki, Vol. 47, No. 2 (2012), 415-420.
LINEAR INDEPENDENCE AND SETS OF UNIQUENESS
Hrvoje Šikić and Ivana Slamić
Department of Mathematics,
University of Zagreb,
Bijenička 30, 10 000 Zagreb,
Croatia
e-mail: hsikic@math.hr
Department of Mathematics,
University of Rijeka,
Omladinska 14, 51000 Rijeka,
Croatia
e-mail: islamic@math.uniri.hr
Abstract. Consider the Bessel system of integer translates {ψk} of a square integrable function ψ. We show that lp-linear independence of {ψk} is equivalent to periodization function pψ(ξ)=∑k Z|
Z|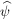 (ξ+k)|2 vanishing almost everywhere on a set which is an lp-set of uniqueness, where 1≤ p≤ 2. General result, concerning no restriction on Bessel systems is then proved for the case p=1.
(ξ+k)|2 vanishing almost everywhere on a set which is an lp-set of uniqueness, where 1≤ p≤ 2. General result, concerning no restriction on Bessel systems is then proved for the case p=1.
2010 Mathematics Subject Classification.
42C15, 46E30.
Key words and phrases. Integer translates, lp-linear independence, sets of uniqueness.
Full text (PDF) (free access)
DOI: 10.3336/gm.47.2.14
References:
-
M. Bownik and D. Speegle,
Linear independence of Parseval wavelets, Illinois J. Math. 54 (2010), 771-785.
MathSciNet
CrossRef
-
L. Colzani,
Existence of sets of uniqueness of lp for general orthonormal systems,
Proc. Amer. Math. Soc. 83 (1981), 569-572.
MathSciNet
CrossRef
-
I. Daubechies,
The wavelet transform, time-frequency localization and signal analysis,
IEEE Trans. Inform. Theory 39 (1990), 961-1005.
MathSciNet
CrossRef
-
E. Hernández, H. Šikić, G. Weiss and E. N. Wilson,
Cyclic subspaces for unitary representations of LCA groups; generalized Zak transform,
Colloq. Math. 118 (2010), 313-332.
MathSciNet
CrossRef
-
E. Hernández, H. Šikić, G. Weiss and E. N. Wilson,
On the properties of the integer translates of a square integrable function, Contemp. Math. 505 (2010), 233-249.
MathSciNet
CrossRef
-
E. Hernández and G. Weiss,
A first course on wavelets, CRC Press, Boca Raton, 1996.
MathSciNet
CrossRef
-
I. I. Hirschman and Y. Katznelson,
Sets of uniqueness and multiplicity for lp,α,
Israel J. Math. 3 (1965), 221-231.
MathSciNet
CrossRef
-
Y. Katznelson,
An introduction to harmonic analysis, 3rd ed.,
Cambridge University Press, Cambridge, 2004.
MathSciNet
CrossRef
-
Y. Katznelson,
Sets of uniqueness for some classes of trigonometrical series,
Bull. Amer. Math. Soc. 70 (1964), 722-723.
MathSciNet
CrossRef
-
S. V. Kislyakov,
A sharp correction theorem,
Studia Math. 113 (1995), 177-196.
MathSciNet
-
M. Nielsen and H. Šikić,
Schauder bases of integer translates,
Appl. Comput. Harmon. Anal. 23 (2007), 259-262.
MathSciNet
CrossRef
-
S. Saliani,
l2-linear independence for the system of integer translates of a square integrable function, to appear in Proc. Amer. Math. Soc.
-
H. Šikić and D. Speegle,
Dyadic PFW's and W0-bases,
Functional Analysis IX, Various Publ. Ser. (Aarhus), 48, Univ. Aarhus, Aarhus, 2007, 85-90.
MathSciNet
-
H. Šikić, D. Speegle and G. Weiss,
Structure of the set of dyadic PFW's,
Contemp. Math. 451 (2008), 263-291.
MathSciNet
CrossRef
-
I. Singer,
Bases in Banach Spaces I,
Springer-Verlag, New-York, 1970.
MathSciNet
-
S. A. Vinogradov,
A strengthening of Kolmogorov's theorem on the conjugate function and interpolational properties of uniformly converging power series,
Trudy Mat. Inst. Steklov. 155 (1981), 7-40 (in Russian); Engl.transl.: Proc.Stecklov Inst. Math. 155 (1981) 3-37.
MathSciNet
-
A. Zygmund,
Trigonometric series, 2nd ed.,
Cambridge University Press, Cambridge, 1959.
MathSciNet
Glasnik Matematicki Home Page
 Z|
Z|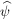 (ξ+k)|2 vanishing almost everywhere on a set which is an lp-set of uniqueness, where 1≤ p≤ 2. General result, concerning no restriction on Bessel systems is then proved for the case p=1.
(ξ+k)|2 vanishing almost everywhere on a set which is an lp-set of uniqueness, where 1≤ p≤ 2. General result, concerning no restriction on Bessel systems is then proved for the case p=1.
 Z|
Z|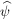 (ξ+k)|2 vanishing almost everywhere on a set which is an lp-set of uniqueness, where 1≤ p≤ 2. General result, concerning no restriction on Bessel systems is then proved for the case p=1.
(ξ+k)|2 vanishing almost everywhere on a set which is an lp-set of uniqueness, where 1≤ p≤ 2. General result, concerning no restriction on Bessel systems is then proved for the case p=1.