Glasnik Matematicki, Vol. 47, No. 2 (2012), 285-293.
ON THE NUMBER OF DIVISORS OF n! AND OF THE FIBONACCI NUMBERS
Florian Luca and Paul Thomas Young
Instituto de Matemáticas,
Universidad Nacional Autónoma de México,
C.P. 58089, Morelia, Michoacán,
México
and
The John Knopfmacher Centre,
for Applicable Analysis and Number Theory,
University of the Witwatersrand,
P.O. Wits 2050,
South Africa
e-mail: fluca@matmor.unam.mx
Department of Mathematics,
College of Charleston,
Charleston, SC 29424,
USA
e-mail: paul@math.cofc.edu
Abstract. Let d(m) be the number of divisors of the positive integer m. Here, we show that if n 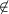 {3,5}, then d(n!) is a divisor of n!. We also show that the only positive integers n such that d(Fn) divides Fn, where Fn is the nth Fibonacci number, are n
{3,5}, then d(n!) is a divisor of n!. We also show that the only positive integers n such that d(Fn) divides Fn, where Fn is the nth Fibonacci number, are n {1,2,3,6,24,48}.
{1,2,3,6,24,48}.
2010 Mathematics Subject Classification.
11N37, 11B39.
Key words and phrases. Divisors, factorials, Fibonacci numbers.
Full text (PDF) (free access)
DOI: 10.3336/gm.47.2.05
References:
- D. Baczkowski, M. Filaseta, F. Luca and O. Trifonov, On rational values of τ(n!)/m!, φ(n!)/m!
and σ(n!)/m!, Int. J. Number Theory 6 (2010), 1199-1214.
MathSciNet
CrossRef
- K. Broughan, M. González, R. Lewis, F. Luca, V. J. Mejía Huguet and A. Togbé, There are no multiply-perfect Fibonacci numbers, Integers 11A (2011), A7.
%ne mogu naci
- J. H. E. Cohn, Fibonacci square numbers, etc., Fibonacci Quarterly 2 (1964), 109-113.
MathSciNet
- J. H. E. Cohn, Lucas and Fibonacci numbers and some Diophantine equations, Proc. Glasgow Math. Assoc. 7 (1965), 24-28.
MathSciNet
CrossRef
- P. Erdős, S. W. Graham, A. Ivić and C. Pomerance, On the divisors of n!, in Analytic Number Theory, Proceedings of a Conference in Honor of Heini Halberstam, Vol. 1, B. Berndt, H. Diamond, A. Hildebrand, eds., Birkhauser, Boston, 1996, 337-355.
MathSciNet
- F. Luca, Equations involving arithmetic functions of
factorials, Divulg. Mat. 8 (2000), 15-23.
MathSciNet
- J. B. Rosser and L. Schoenfeld, Approximate formulas for some func-
tions of prime numbers, Illinois J. Math. 6 (1962), 64-94.
MathSciNet
CrossRef
- C. Spiro, How often is the number of divisors of n a divisor of n?, J. Number Theory 21 (1985), 81-100.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
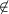 {3,5}, then d(n!) is a divisor of n!. We also show that the only positive integers n such that d(Fn) divides Fn, where Fn is the nth Fibonacci number, are n
{3,5}, then d(n!) is a divisor of n!. We also show that the only positive integers n such that d(Fn) divides Fn, where Fn is the nth Fibonacci number, are n {1,2,3,6,24,48}.
{1,2,3,6,24,48}.
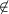 {3,5}, then d(n!) is a divisor of n!. We also show that the only positive integers n such that d(Fn) divides Fn, where Fn is the nth Fibonacci number, are n
{3,5}, then d(n!) is a divisor of n!. We also show that the only positive integers n such that d(Fn) divides Fn, where Fn is the nth Fibonacci number, are n {1,2,3,6,24,48}.
{1,2,3,6,24,48}.