Glasnik Matematicki, Vol. 47, No. 2 (2012), 277-284.
ELLIPTIC CURVES OVER QUADRATIC FIELDS WITH FIXED TORSION SUBGROUP AND POSITIVE RANK
Mirela Jukić Bokun
Department of Mathematics, University of Osijek, Trg Ljudevita Gaja 6, 31 000 Osijek, Croatia
e-mail: mirela@mathos.hr
Abstract. For each of the torsion groups Z/2Z 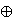 Z/10Z,
Z/2Z
Z/10Z,
Z/2Z 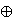 Z/12Z, Z/15Z we find the quadratic field with the smallest absolute value of its discriminant
such that there exists an elliptic curve with that torsion and positive rank.
For the torsion groups Z/11Z, Z/14Z we solve the analogous problem after assuming the Parity conjecture.
Z/12Z, Z/15Z we find the quadratic field with the smallest absolute value of its discriminant
such that there exists an elliptic curve with that torsion and positive rank.
For the torsion groups Z/11Z, Z/14Z we solve the analogous problem after assuming the Parity conjecture.
2010 Mathematics Subject Classification.
11G05, 14H52, 11R11.
Key words and phrases. Elliptic curve, torsion group, rank, quadratic field.
Full text (PDF) (free access)
DOI: 10.3336/gm.47.2.04
References:
-
W. Bosma, J. Cannon and C. Playoust, The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), 235-265.
Magma
CrossRef
-
J. Bosman, P. Bruin, A. Dujella and F. Najman, Ranks of elliptic curves with prescribed torsion over number fields, preprint.
-
J. E. Cremona, Algorithms for Modular Elliptic Curves, Cambridge
University Press, 1997.
MathSciNet
-
T. Dokchitser, Notes on the Parity Conjecture,
to appear in a CRM Advanced Courses volume, Birkhauser.
-
A. Dujella and M. Jukić Bokun, On the rank of elliptic curves over
Q(i) with torsion group Z/4Z ×
Z/4Z, Proc. Japan Acad. Ser. A Math. Sci. 86 (2010), 93-96.
MathSciNet
CrossRef
-
M. Jukić Bokun, On the rank of elliptic curves over Q((-3)1/2)
with torsion groups Z/3Z × Z/3Z and Z/3Z × Z/6Z,
Proc. Japan Acad. Ser. A Math. Sci. 87 (2011), 61-64.
MathSciNet
CrossRef
-
S. Kamienny, Torsion points on elliptic curves and q-coefficients of
modular forms, Invent. Math. 109 (1992), 221-229.
MathSciNet
CrossRef
-
S. Kamienny and F. Najman, Torsion groups of elliptic curves over quadratic
fields, Acta. Arith. 152 (2012), 291-305.
MathSciNet
CrossRef
-
M. A. Kenku and F. Momose, Torsion points on elliptic curves defined over
quadratic fields, Nagoya Math. J. 109 (1988), 125-149.
MathSciNet
CrossRef
-
L. Kulesz, Families of elliptic curves of high rank with nontrivial
torsion group over Q, Acta Arith. 108 (2003), 339-356.
MathSciNet
CrossRef
-
B. Mazur, Rational isogenies of prime degree, Invent. Math.
44 (1978), 129-162.
MathSciNet
CrossRef
-
F. P. Rabarison, Structure de torsion des courbes elliptiques sur les
corps quadratiques, Acta Arith. 144 (2010), 17-52.
MathSciNet
CrossRef
-
D. Simon, Le fichier gp.
link
Glasnik Matematicki Home Page
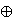 Z/10Z,
Z/2Z
Z/10Z,
Z/2Z 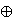 Z/12Z, Z/15Z we find the quadratic field with the smallest absolute value of its discriminant
such that there exists an elliptic curve with that torsion and positive rank.
For the torsion groups Z/11Z, Z/14Z we solve the analogous problem after assuming the Parity conjecture.
Z/12Z, Z/15Z we find the quadratic field with the smallest absolute value of its discriminant
such that there exists an elliptic curve with that torsion and positive rank.
For the torsion groups Z/11Z, Z/14Z we solve the analogous problem after assuming the Parity conjecture.