Glasnik Matematicki, Vol. 47, No. 1 (2012), 207-223.
ON EXACTNESS OF THE COARSE SHAPE GROUP SEQUENCE
Nikola Koceić Bilan
Department of Mathematics, University of Split,
Teslina 12/III, 21000 Split,
Croatia
e-mail: koceic@pmfst.hr
Abstract. The coarse shape groups are recently introduced. Given a pointed pair
(X,X0,x0) and a k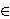 N, the relative coarse
shape group π*k(X,X0,x0), having the
standard relative shape group πk(X,X0,x0)
for its subgroup, is defined. They establish a functorial relations of the
topological, homotopy and (coarse) shape category to the category of groups.
Therefore, the coarse shape groups are new algebraic topological, homotopy and
(coarse) shape type invariants. For every pointed pair of metric compacta
(X,X0,x0) and for every k>1, the boundary homomorphism
∂k*:π*k (X,X0,x0)
→ π*k-1 (X0,x0) = π*
k-1(X0, {x0},x0) is
introduced which induces a natural transformation. The corresponding sequence
of the coarse shape groups is exact, although the shape sequence generally
failed to be exact. This exactness makes powerful tool for computing coarse
shape groups of some particular pointed pairs of metric compacta.
N, the relative coarse
shape group π*k(X,X0,x0), having the
standard relative shape group πk(X,X0,x0)
for its subgroup, is defined. They establish a functorial relations of the
topological, homotopy and (coarse) shape category to the category of groups.
Therefore, the coarse shape groups are new algebraic topological, homotopy and
(coarse) shape type invariants. For every pointed pair of metric compacta
(X,X0,x0) and for every k>1, the boundary homomorphism
∂k*:π*k (X,X0,x0)
→ π*k-1 (X0,x0) = π*
k-1(X0, {x0},x0) is
introduced which induces a natural transformation. The corresponding sequence
of the coarse shape groups is exact, although the shape sequence generally
failed to be exact. This exactness makes powerful tool for computing coarse
shape groups of some particular pointed pairs of metric compacta.
2010 Mathematics Subject Classification.
55P55, 55Q05, 55N99.
Key words and phrases. Polyhedron, inverse system, pro-category, pro*-category, expansion,
shape, coarse shape, homotopy group, shape group, coarse shape group, exactness.
Full text (PDF) (free access)
DOI: 10.3336/gm.47.1.19
References:
- J. Keesling and S. Mardešić, A shape fibration
with fibers of different shape, Pacific J. Math. 84 (1979), 319-331.
MathSciNet
CrossRef
- N. Koceić Bilan and N. Uglešić, The coarse
shape, Glas. Mat. Ser. III. 42(62) (2007), 145-187.
MathSciNet
CrossRef
- N. Koceić Bilan, On some coarse shape invariants,
Topology Appl. 157 (2010), 2679-2685.
MathSciNet
CrossRef
- N. Koceić Bilan, The coarse shape groups, Topology
Appl. 157 (2010), 894-901.
MathSciNet
CrossRef
- S. Mardešić and J. Segal, Shape theory,
North-Holland, North-Holland Publishing Co., Amsterdam, 1982.
MathSciNet
- N. Uglešić and B. Červar, The concept of a
weak shape type, Int. J. Pure Appl. Math. 39
(2007), 363-428.
MathSciNet
- N. Uglešić, Stability is a weak shape invariant,
Glas. Mat. Ser. III 44(64) (2009), 241-254.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
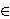 N, the relative coarse
shape group π*k(X,X0,x0), having the
standard relative shape group πk(X,X0,x0)
for its subgroup, is defined. They establish a functorial relations of the
topological, homotopy and (coarse) shape category to the category of groups.
Therefore, the coarse shape groups are new algebraic topological, homotopy and
(coarse) shape type invariants. For every pointed pair of metric compacta
(X,X0,x0) and for every k>1, the boundary homomorphism
∂k*:π*k (X,X0,x0)
→ π*k-1 (X0,x0) = π*
k-1(X0, {x0},x0) is
introduced which induces a natural transformation. The corresponding sequence
of the coarse shape groups is exact, although the shape sequence generally
failed to be exact. This exactness makes powerful tool for computing coarse
shape groups of some particular pointed pairs of metric compacta.
N, the relative coarse
shape group π*k(X,X0,x0), having the
standard relative shape group πk(X,X0,x0)
for its subgroup, is defined. They establish a functorial relations of the
topological, homotopy and (coarse) shape category to the category of groups.
Therefore, the coarse shape groups are new algebraic topological, homotopy and
(coarse) shape type invariants. For every pointed pair of metric compacta
(X,X0,x0) and for every k>1, the boundary homomorphism
∂k*:π*k (X,X0,x0)
→ π*k-1 (X0,x0) = π*
k-1(X0, {x0},x0) is
introduced which induces a natural transformation. The corresponding sequence
of the coarse shape groups is exact, although the shape sequence generally
failed to be exact. This exactness makes powerful tool for computing coarse
shape groups of some particular pointed pairs of metric compacta.