Glasnik Matematicki, Vol. 47, No. 1 (2012), 181-186.
THE SPECIAL HYPERSURFACES OF MINKOWSKI SPACE
Jintang Li
School of Mathematical Sciences,
Xiamen University,
361005 Xiamen, Fujian,
China
e-mail: dli66@xmu.edu.cn
Abstract. Let x:(Mn,F) 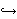 (Vn+1, F̄) be a simply connected hypersurface in a
Minkowski space (Vn+1, F̄). In this paper, using the
Gauss formula of Chern connection on Finsler submanifolds, we shall
prove that if x(p) is normal to Tp(M) (∀ p
(Vn+1, F̄) be a simply connected hypersurface in a
Minkowski space (Vn+1, F̄). In this paper, using the
Gauss formula of Chern connection on Finsler submanifolds, we shall
prove that if x(p) is normal to Tp(M) (∀ p M), then
M with the induced metric is isometric to the standard Euclidean
sphere.
M), then
M with the induced metric is isometric to the standard Euclidean
sphere.
2010 Mathematics Subject Classification.
53C60, 53C40.
Key words and phrases. Finsler manifolds, Gauss formula, Minkowski space.
Full text (PDF) (free access)
DOI: 10.3336/gm.47.1.16
References:
- D. Bao and S. S. Chern, On a notable connection in Finsler
geometry, Houston J. Math. 19 (1993), 135-180.
MathSciNet
- D. Bao, S. S. Chern and Z. Shen, An introduction to Riemann-Finsler geometry,
Springer-Verlag, 2000.
MathSciNet
CrossRef
- S. S. Chern, Local equivalence and Euclidean connection in Finsler
spaces, Sci. Rep. Nat. Tsing Hua Univ. Ser. A. 5 (1948), 95-121.
MathSciNet
- J. T. Li, The fundamental formulas of Finsler submanifolds, Bull. Korean Math. Soc. 47 (2010), 767-775.
MathSciNet
CrossRef
- Z. Shen, On Finsler geometry of
submanifolds, Math. Ann. 311 (1998), 549-576.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
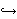 (Vn+1, F̄) be a simply connected hypersurface in a
Minkowski space (Vn+1, F̄). In this paper, using the
Gauss formula of Chern connection on Finsler submanifolds, we shall
prove that if x(p) is normal to Tp(M) (∀ p
(Vn+1, F̄) be a simply connected hypersurface in a
Minkowski space (Vn+1, F̄). In this paper, using the
Gauss formula of Chern connection on Finsler submanifolds, we shall
prove that if x(p) is normal to Tp(M) (∀ p M), then
M with the induced metric is isometric to the standard Euclidean
sphere.
M), then
M with the induced metric is isometric to the standard Euclidean
sphere.