Glasnik Matematicki, Vol. 47, No. 1 (2012), 133-142.
THE GENERATING CONDITION FOR THE EXTENSION OF THE CLASSICAL GAUSS SERIES-PRODUCT IDENTITY
Tomislav Šikić
Faculty of Electrical Engineering and Computing, University of Zagreb, Unska 3, 10000 Zagreb, Croatia
e-mail: tomislav.sikic@fer.hr
Abstract. In this paper a condition is presented on parameters (n1,n2,Λk), for arbitrary partition n={n1, n2}, (n1≤ n2) and k=1,...,n-1, which guarantees that two different interpretations of characters of
fundamental modules L(Λk) for the affine Kac-Moody Lie algebra
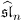 generate extended classical Gauss series-product identities.
generate extended classical Gauss series-product identities.
2010 Mathematics Subject Classification.
17B67.
Key words and phrases. Affine Lie algebras, characters of fundamental modules, series-product identities, classical Gauss identity.
Full text (PDF) (free access)
DOI: 10.3336/gm.47.1.10
References:
- G. E. Andrews, The theory of partitions, Encyclopedia of Mathematics and its Applications 2, Addison-Wesley, Reading MA, 1976.
MathSciNet
- W. J. Cook, H.-S. Li and K. C. Misra,
A recurrence relation
for characters of highest weight integrable modules for affine Lie
algebras,
Commun. Contemp. Math. 9 (2007), 121-133.
MathSciNet
CrossRef
- A. J. Feingold and J. Lepowsky,
The Weyl-Kac character
formula and power series identities,
Adv. in Math. 29 (1978), 271-309.
MathSciNet
CrossRef
- V. G. Kac,
Infinite dimensional Lie algebras, third edition, Cambridge University Press, Cambridge, 1990.
MathSciNet
CrossRef
- V. G. Kac,
Infinite-dimensional Lie algebras and
Dedekind's η-function, classical Möbious function and
the very strange formula,
Adv. in Math. 30 (1978), 85-136.
MathSciNet
CrossRef
- V. G. Kac, and D. H. Peterson,
Infinite-dimensional Lie algebras, theta functions and modular forms,
Adv. in Math. 53 (1984), 125-264.
MathSciNet
CrossRef
- V. G. Kac, and D. H. Peterson,
112 construction of the basic representation of the loop group of E8,
in: Proceedings of the conference "Anomalies, geometry, topology", World Sci., Argone 1985, 276-298.
MathSciNet
- F. ten Kroode and J. van de Leur,
Bosonic and fermionic realization of the affine algebra
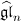 ,
Comm. Math. Phys. 137 (1991), 67-107.
,
Comm. Math. Phys. 137 (1991), 67-107.
MathSciNet
CrossRef
- T. Šikić,
An extension of the classical Gauss series-product identity by boson-fermionic realization of the affine algebra
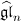 ,
J. Algebra Appl. 9 (2010), 123-133.
,
J. Algebra Appl. 9 (2010), 123-133.
MathSciNet
CrossRef
- T. Šikić,
Some series-product identities and boson-fermionic realization of the
affine Lie algebra
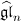 ,
in: 4th Croatian Mathematical Congres, Osijek, Croatia, 2008.
,
in: 4th Croatian Mathematical Congres, Osijek, Croatia, 2008.
Glasnik Matematicki Home Page
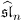 generate extended classical Gauss series-product identities.
generate extended classical Gauss series-product identities.
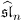 generate extended classical Gauss series-product identities.
generate extended classical Gauss series-product identities.
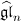 ,
Comm. Math. Phys. 137 (1991), 67-107.
,
Comm. Math. Phys. 137 (1991), 67-107.
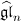 ,
J. Algebra Appl. 9 (2010), 123-133.
,
J. Algebra Appl. 9 (2010), 123-133.
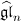 ,
in: 4th Croatian Mathematical Congres, Osijek, Croatia, 2008.
,
in: 4th Croatian Mathematical Congres, Osijek, Croatia, 2008.