Glasnik Matematicki, Vol. 46, No. 2 (2011), 385-414.
NORMALIZERS AND SELF-NORMALIZING SUBGROUPS
Boris Širola
Department of Mathematics, University of Zagreb, Bijenička 30, 10000 Zagreb, Croatia
e-mail: sirola@math.hr
Abstract. Let K be a field, char(K) ≠ 2. Suppose
G=G(K) is the group of K-points of
a reductive algebraic K-group G. Let
G1≤ G be the group of K-points of a reductive
subgroup G1≤ G. We study the
structure of the normalizer N= NG(G1). In
particular, let G= SL(2n, K) for n>1. For certain well
known embeddings of G1 into G, where G1= Sp(2n, K) or SO(2n, K), we show that N/G1 ≅
μk(K), the group of k-th roots of unity
in K. Here, k=2n if certain Condition (◊)
holds, and k=n if not. Moreover, there is a precisely defined
subgroup N' of N such that
N/N' ≅ Z/2 Z if
Condition (◊) holds, and
N=N' if not. Furthermore,
when n>1,
as the main
observations of the paper we have the following: (i) N is
a self-normalizing subgroup of G; (ii) N' ≅
G1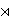 Z[X] μn (K), the semidirect product
of G1 by μn (K). Besides we point out
that analogous results will hold for a number of other pairs of
groups (G,G1). We also show that for the pair (g, g1), of the corresponding K-Lie algebras,
g1 is self-normalizing in g; which
generalizes a well-known result in the zero characteristic.
Z[X] μn (K), the semidirect product
of G1 by μn (K). Besides we point out
that analogous results will hold for a number of other pairs of
groups (G,G1). We also show that for the pair (g, g1), of the corresponding K-Lie algebras,
g1 is self-normalizing in g; which
generalizes a well-known result in the zero characteristic.
2000 Mathematics Subject Classification.
20E34, 20G15, 17B05, 17B20.
Key words and phrases. Normalizer, self-normalizing subgroup, symmetric pair,
symplectic group, even orthogonal group.
Full text (PDF) (free access)
DOI: 10.3336/gm.46.2.10
References:
- E. Artin, Geometric Algebra, Interscience,
New York, 1957.
MathSciNet
- A. Borel, Linear Algebraic groups. Second Enlarged
Edition, Graduate Texts in Math., Vol. 126, Springer-Verlag, New
York, 1991.
MathSciNet
- N. Bourbaki, Lie groups and Lie algebras,
Chapters 1-3, Springer-Verlag, Berlin, 1989.
MathSciNet
- N. Bourbaki, Groupes et Algèbres de Lie,
Chapitres VII, VIII, Hermann, Paris, 1975.
- R. Brylinski and B. Kostant,
Nilpotent orbits, normality, and Hamiltonian group actions, J.
Amer. Math. Soc. 7 (1994), 269-298.
MathSciNet
CrossRef
- R. Carter, Finite groups of Lie type. Conjugacy classes
and complex characters, Wiley-Interscience, Chichester, 1993.
MathSciNet
- C. Chevalley, Sur certains groupes simples,
Tôhoku Math. J (2) 7 (1955), 14-66.
MathSciNet
CrossRef
- J. Dixmier, Enveloping Algebras, Graduate Studies in
Mathematics 11, Amer. Math. Soc., 1996.
MathSciNet
- E. B. Dynkin, Semisimple subalgbras of semisimple Lie
algebras, Amer. Math. Soc. Translations (2) 6 (1957),
111-244.
- E. B. Dynkin, Maximal subgroups of the classical groups,
Amer. Math. Soc. Translations (2) 6 (1957), 245-378.
- R. Goodman and N. R. Wallach, Representations
and Invariants of the Classical Groups, Encyclopedia of Mathematics
and its Applications, Vol. 68, Cambridge Univ. Press, Cambridge,
1998.
MathSciNet
- R. Howe, E.-C. Tan and J. F. Willenbring,
Stable branching rules for classical symmetric pairs, Trans.
Amer. Math. Soc. 357 (2005), 1601-1626.
MathSciNet
CrossRef
- J. E. Humphreys, Conjugacy Classes in Semisimple
Algebraic Groups, Mathematical Surveys and Monographs, Vol. 43,
Amer. Math. Soc., Providence, 1995.
MathSciNet
- J. C. Jantzen, Nilpotent orbits in
representation theory, Lie Theory, Progr. Math., Vol. 228, Birkhäuser, Boston (2004), pp. 1-211.
MathSciNet
- A. W. Knapp, Geometric interpretations of two branching
theorems of D. E. Littlewood, J. Algebra 270 (2003),
728-754.
MathSciNet
CrossRef
- T. Kobayashi, Discrete decomposability of the restriction
of A q(λ ) with respect to reductive subgroups
III. Restriction of Harish-Chandra modules and associated
varieties, Invent. Math. 131 (1998), 229-256.
MathSciNet
CrossRef
- T. Kobayashi, Discretely decomposable restrictions
of unitary representations of reductive Lie groups-examples and
conjectures, Analysis on homogeneous spaces and representation
theory of Lie groups, Okayama-Kyoto (1997), 99-127, Adv. Stud. Pure
Math. 26, Math. Soc. Japan, Tokyo, 2000.
MathSciNet
- N. Koblitz, A course in number theory and
cryptography, 2nd ed., Graduate Texts in Math., Vol. 114,
Springer-Verlag, Berlin, 1994.
MathSciNet
- B. Kostant, A branching law for subgroups fixed by an
involution and a noncompact analogue of the Borel-Weil theorem,
Noncommutative harmonic analysis, Progress in Math., vol. 220,
Birkhäuser Boston, Boston, 2004, pp 291-353.
MathSciNet
- T. Levasseur and S. P. Smith,
Primitive ideals and nilpotent orbits in type G2, J.
Algebra 114 (1988), 81-105.
MathSciNet
CrossRef
- R. W. Richardson, Jr., Conjugacy classes in Lie
algebras and algebraic groups, Ann. of Math. (2) 86
(1967), 1-15.
MathSciNet
CrossRef
- G. M. Seitz, The maximal subgroups of classical algrebraic
groups, Mem. Amer. Math. Soc., 67 No. 365 (1987).
MathSciNet
- B. Širola, On pairs of complex Lie groups and
generalized global Cartan decomposition, Grazer Math. Ber.
348 (2005), 79-90.
MathSciNet
- B. Širola, A generalized global Cartan decomposition:
a basic example, Comm. Algebra 34 (2006), 3267-3279.
MathSciNet
CrossRef
- B. Širola, Pairs of semisimple Lie algebras and their
maximal reductive subalgebras, Algebr. Represent. Theory
11 (2008), 233-250.
MathSciNet
CrossRef
- B. Širola, Pairs of Lie algebras and their
self-normalizing reductive subalgebras, J. Lie Theory 19
(2009), 735-766.
MathSciNet
- B. Širola, Normalizers and self-normalizing subgroups II,
Cent. Eur. J. Math. 9 (2011), 1317-1332.
- B. Širola, On centralizers and normalizers for groups,
preprint.
- T. A. Springer and R. Steinberg, Conjugacy
classes, Seminar on Algebraic Groups and Related Finite Groups (A.
Borel et al. eds.), Lecture Notes in Math., Vol. 131,
Springer-Verlag, Berlin, 1970, pp. 167-266.
MathSciNet
- D. A. Vogan, Jr., The unitary dual of G2,
Invent. Math. 116 (1994), 677-791.
MathSciNet
CrossRef
- A. Wagner, On the clssification of the classical groups,
Math. Zeit. 97 (1967), 66-76.
MathSciNet
CrossRef
- G. E. Wall, On the conjugacy classes in the unitary,
symplectic and orthogonal groups, J. Austral. Math. Soc.
3 (1963), 1-62.
MathSciNet
Glasnik Matematicki Home Page
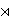 Z[X] μn (K), the semidirect product
of G1 by μn (K). Besides we point out
that analogous results will hold for a number of other pairs of
groups (G,G1). We also show that for the pair (g, g1), of the corresponding K-Lie algebras,
g1 is self-normalizing in g; which
generalizes a well-known result in the zero characteristic.
Z[X] μn (K), the semidirect product
of G1 by μn (K). Besides we point out
that analogous results will hold for a number of other pairs of
groups (G,G1). We also show that for the pair (g, g1), of the corresponding K-Lie algebras,
g1 is self-normalizing in g; which
generalizes a well-known result in the zero characteristic.