Glasnik Matematicki, Vol. 46, No. 2 (2011), 311-323.
THE D(-k2)-TRIPLE {1,k2+1,k2+4} WITH k PRIME
Alan Filipin and Yasutsugu Fujita
Faculty of Civil Engineering,
University of Zagreb,
Fra Andrije Kačića-Miošića 26, 10 000 Zagreb,
Croatia
e-mail: filipin@grad.hr
Department of Mathematics, College of Industrial Technology,
Nihon University,
2-11-1 Shin-ei, Narashino,
Chiba,
Japan
e-mail: fujita.yasutsugu@nihon-u.ac.jp
Abstract. Let n be a nonzero integer. A set of m distinct positive
integers is called a D(n)-m-tuple if the product of any two of
them increased by n is a perfect square. Let k be a prime
number. In this paper we prove that the D(-k2)-triple
{1,k2+1,k2+4} cannot be extended to a D(-k2)-quadruple if
k≠3. And for k=3 we prove that if the set {1,10,13,d} is
a D(-9)-quadruple, then d=45.
2000 Mathematics Subject Classification.
11D09, 11J68.
Key words and phrases. Diophantine tuples, simultaneous Diophantine equations.
Full text (PDF) (free access)
DOI: 10.3336/gm.46.2.03
References:
- A. Baker and G. Wüstholz, Logarithmic forms
and group varieties, J. Reine Angew. Math. 442 (1993), 19-62.
MathSciNet
CrossRef
- M. A. Bennett, On the number of solutions of simultaneous Pell equations, J. Reine Angew. Math. 498 (1998), 173-199.
MathSciNet
CrossRef
-
M. A. Bennett, M. Cipu, M. Mignotte and R. Okazaki,
On the number of solutions of simultaneous Pell equations II,
Acta Arith. 122 (2006), 407-417.
MathSciNet
CrossRef
- E. Brown, Sets in which xy+k is always a
square, Math. Comp. 45 (1985), 613-620.
MathSciNet
CrossRef
- A. Dujella, Generalization of a problem of
Diophantus, Acta Arith. 65 (1993), 15-27.
MathSciNet
-
A. Dujella, Complete solution of a family of simultaneous
Pellian equations, Acta Math. Inform. Univ. Ostraviensis 6 (1998), 59-67.
MathSciNet
-
A. Dujella, An absolute bound for the size of Diophantine
m-tuples, J. Number Theory 89 (2001), 126-150.
MathSciNet
CrossRef
-
A. Dujella, There are only finitely many Diophantine
quintuples, J. Reine Angew. Math. 566 (2004), 183-214.
MathSciNet
CrossRef
-
A. Dujella, A. Filipin and C. Fuchs,
Effective solution of the D(-1)-quadruple conjecture,
Acta Arith. 128 (2007), 319-338.
MathSciNet
CrossRef
-
A. Dujella and C. Fuchs,
Complete solution of a problem of Diophantus and Euler,
J. London Math. Soc. 71 (2005), 33-52.
MathSciNet
CrossRef
-
A. Dujella and A. Pethö,
A generalization of a theorem of Baker and Davenport, Quart.
J. Math. Oxford Ser. (2) 49 (1998), 291-306.
MathSciNet
CrossRef
- Y. Fujita, The non-extensibility of D(4k)-triples
{1,4k(k-1),4k2+1} with |k| prime, Glas. Mat. Ser. III 41 (2006), 205-216.
MathSciNet
CrossRef
- Y. Fujita, Extensions of the D(
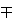 k2)-triples {k2,k2±1,4k2±1}, Period. Math. Hungar.
59 (2009), 81-98.
k2)-triples {k2,k2±1,4k2±1}, Period. Math. Hungar.
59 (2009), 81-98.
MathSciNet
CrossRef
-
Y. Fujita, The number of Diophantine quintuples, Glas. Mat.
Ser. III 45 (2010), 15-29.
MathSciNet
CrossRef
- Y. Fujita and A Togbé, The extension of the D(-k2)-pair
{k2,k2+1}, Period. Math. Hungar., to appear.
- R. A. Mollin, Quadratics, CRC Press, Boca Ranton, 1996.
MathSciNet
- J. E. Shockley, Introduction to Number Theory, Holt, Rinehart and
Winston, 1967.
MathSciNet
Glasnik Matematicki Home Page
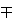 k2)-triples {k2,k2±1,4k2±1}, Period. Math. Hungar.
59 (2009), 81-98.
k2)-triples {k2,k2±1,4k2±1}, Period. Math. Hungar.
59 (2009), 81-98.