Glasnik Matematicki, Vol. 46, No. 2 (2011), 283-309.
DIOPHANTINE m-TUPLES FOR QUADRATIC POLYNOMIALS
Ana Jurasić
Department of Mathematics, University of
Rijeka, Omladinska 14, 51000 Rijeka, Croatia
e-mail: ajurasic@math.uniri.hr
Abstract. In this paper, we prove that there does not exist a set
with more than 98 nonzero polynomials in Z[X], such
that the product of any two of them plus a quadratic polynomial
n is a square of a polynomial from Z[X] (we exclude
the possibility that all elements of such set are constant
multiples of a linear polynomial p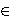 Z[X] such that
p2|n). Specially, we prove that if such a set contains only
polynomials of odd degree, then it has at most 18 elements.
Z[X] such that
p2|n). Specially, we prove that if such a set contains only
polynomials of odd degree, then it has at most 18 elements.
2000 Mathematics Subject Classification.
11C08, 11D99.
Key words and phrases. Diophantine m-tuples, polynomials.
Full text (PDF) (free access)
DOI: 10.3336/gm.46.2.02
References:
- A. Baker and H. Davenport, The equations
3x2-2=y2 and 8x2-7=z2, Quart. J. Math.
Oxford Ser. (2) 20 (1969), 129-137.
MathSciNet
- Diophantus of Alexandria, Arithmetics and the Book
of Polygonal Numbers, (I. G. Bashmakova, Ed.) (Nauka 1974), 85-86,
215-217.
MathSciNet
- A. Dujella, On Diophantine quintuples, Acta
Arith. 81 (1997), 69-79.
MathSciNet
- A. Dujella, On the size of Diophantine m-tuples,
Math. Proc. Cambridge Philos. Soc. 132 (2002),
23-33.
MathSciNet
CrossRef
- A. Dujella, Bounds for the size of sets with the
property D(n), Glas. Mat. Ser. III 39 (2004),
199-205.
MathSciNet
CrossRef
- A. Dujella, There are only finitely many
Diophantine quintuples, J. Reine Angew. Math.
566 (2004), 183-214.
MathSciNet
CrossRef
- A. Dujella and C. Fuchs, A polynomial variant of a
problem of Diophantus and Euler, Rocky Mountain J. Math.
33 (2003), 797-811.
MathSciNet
CrossRef
- A. Dujella and C. Fuchs, Complete solution of the
polynomial version of a problem of Diophantus, J. Number
Theory 106 (2004), 326-344.
MathSciNet
CrossRef
- A. Dujella, C. Fuchs and R. F. Tichy, Diophantine
m-tuples for linear polynomials, Period. Math. Hungar.
45 (2002), 21-33.
MathSciNet
CrossRef
- A. Dujella, C. Fuchs and G. Walsh, Diophantine
m-tuples for linear polynomials. II. Equal degrees, J.
Number Theory, 120 (2006), 213-228.
MathSciNet
CrossRef
- A. Dujella and A. Jurasić, On the size of sets in a polynomial variant of a problem of
Diophantus, Int. J. Number Theory 6 (2010), 1449-1471.
- P. Gibbs, Some rational sextuples, Glas. Mat. Ser. III 41 (2006), 195-203.
MathSciNet
CrossRef
- B. W. Jones, A variation of a problem of Davenport
and Diophantus, Quart. J. Math. Oxford Ser.(2)
27 (1976), 349-353.
MathSciNet
- B. W. Jones, A second variation of a problem of
Davenport and Diophantus, Fibonacci Quart. 15
(1978), 155-165.
MathSciNet
- R. C. Mason, Diophantine equations over function
fields, London Mathematical Society Lecture Notes Series,
vol. 96, Cambridge University Press, Cambridge, 1984.
MathSciNet
Glasnik Matematicki Home Page
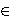 Z[X] such that
p2|n). Specially, we prove that if such a set contains only
polynomials of odd degree, then it has at most 18 elements.
Z[X] such that
p2|n). Specially, we prove that if such a set contains only
polynomials of odd degree, then it has at most 18 elements.
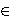 Z[X] such that
p2|n). Specially, we prove that if such a set contains only
polynomials of odd degree, then it has at most 18 elements.
Z[X] such that
p2|n). Specially, we prove that if such a set contains only
polynomials of odd degree, then it has at most 18 elements.