Glasnik Matematicki, Vol. 46, No.1 (2011), 167-188.
VARIATIONAL CHARACTERISATION OF NODAL SOLUTIONS OF A STURM-LIOUVILLE PROBLEM WITH STRONG NONLINEARITY
Lavoslav Čaklović
Faculty of Natural Sciences,
Department of Mathematics,
University of Zagreb,
10000 Zagreb,
Croatia
e-mail: caklovic@math.hr
Abstract. We consider sublinear Sturm-Liouville problem
-u''+ψ(t) |u |p-1 u =λ u, p>1,
u(0)=u(1)=0
where ψ is positive and continuous. Using the Nehari variational
technique and critical point theory we prove that for each n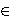 N there is
unique (up to the sign) n-nodal solution of the b.v.p. which is
the critical point of a restricted functional associated to the problem.
N there is
unique (up to the sign) n-nodal solution of the b.v.p. which is
the critical point of a restricted functional associated to the problem.
2000 Mathematics Subject Classification.
34C25, 47H15, 58E05, 58F05, 70H30.
Key words and phrases. Critical point theory, Palais-Smale condition, Sturm-Liouville problem, nodal solutions.
Full text (PDF) (free access)
DOI: 10.3336/gm.46.1.14
References:
-
H. Berestycki, Le nombre de solutions de certains problèmes
semi-linéaires ellipti\-ques, J. Funct. Anal. 40 (1980), 1-29.
MathSciNet
CrossRef
-
C.-N. Chen, Multiple solutions for a class of nonlinear
Sturm-Liouville problems on the half line, J. Differential
Equations 85 (1990), 236-275.
MathSciNet
CrossRef
-
C.-N. Chen, Uniqueness and bifurcation for solutions of nonlinear Sturm-Liouville eigenvalue problems, Arch. Rational Mech. Anal. 111 (1990), 51-85.
MathSciNet
CrossRef
-
C.-N. Chen, Multiple solutions for a class of nonlinear
Sturm-Liouville problems when nonlinearities are not odd,
J. Differential Equations 89 (1991), 138-153.
MathSciNet
CrossRef
-
E. A. Coddington and N. Levinson, Theory of ordinal differential
equations, McGraw-Hill, New York, 1955.
MathSciNet
-
C. V. Coffman, A minimum-maximum principle for a class of non-linear integral equations, J. Analyse Math. 22 (1969), 391-419.
MathSciNet
CrossRef
-
C. V. Coffman, On variational principles for sublinear boundary value
problems, J. Differential Equations 17 (1975), 46-60.
MathSciNet
CrossRef
-
H. P. Heinz, Free Ljusternik-Schnirelman theory and the bifurcation
diagrams of certain singular nonlinear problems, J. Differential Equations
66 (1987), 263-300.
MathSciNet
CrossRef
-
H. P. Heinz, Nodal properties and bifurcation from the essential spectrum for
a class of nonlinear Sturm-Liouville problems, J. Differential Equations
64 (1986), 79-108.
MathSciNet
CrossRef
-
H. P. Heinz, Nodal properties and variational characterizations of solutions
to nonlinear Sturm-Liouville problems, J. Differential Equations
62 (1986), 299-333.
MathSciNet
CrossRef
-
H. P. Heinz, Free Ljusternik-Schnirelman theory and the bifurcation
diagrams of certain singular nonlinear problems, J. Differential Equations
66 (1987), 263-300.
MathSciNet
CrossRef
-
J. A. Hempel, Multiple solutions for a class of nonlinear boundary value problems, Indiana University Mathematical Journal
20 (1970/1971), 983-996.
MathSciNet
CrossRef
-
Z. Nehari, Characteristic values associated with a class of non-linear second-order differential equations, Acta. Math. 105 (1961),
141-175.
MathSciNet
CrossRef
-
P. H. Rabinowitz, Minimax methods in critical point theory with
application to differential equation, CBMS Reg. Conf. Ser. in Math.
65, AMS, Providence, Rhode Island, 1986.
MathSciNet
-
T. Weth, Spectral and variational characterizations of solutions to
semilinear eigenvalue problems, Ph.D. thesis, Johannes
Gutenberg-Universität, Mainz, 2001.
Glasnik Matematicki Home Page
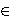 N there is
unique (up to the sign) n-nodal solution of the b.v.p. which is
the critical point of a restricted functional associated to the problem.
N there is
unique (up to the sign) n-nodal solution of the b.v.p. which is
the critical point of a restricted functional associated to the problem.