Glasnik Matematicki, Vol. 46, No.1 (2011), 31-41.
EQUATIONS RELATED TO DERIVATIONS ON PRIME RINGS
Maja Fošner and Joso Vukman
Faculty of logistics, University of Maribor, Mariborska cesta 2, 3000 Celje, Slovenia
e-mail: maja.fosner@uni-mb.si
Department of Mathematics and Computer Science,
Faculty of natural sciences and mathematics,
University of Maribor,
Koroška cesta 160, SI-2000 Maribor,
Slovenia
e-mail: joso.vukman@uni-mb.si
Dedicated to the memory of Professor Svetozar Kurepa
Abstract. In this paper we prove the following result. Let m ≥
0 and n ≥ 0 be integers with m+n ≠ 0 and let R be a prime
ring with char(R)=0 or m+n+1 ≤ char(R) ≠ 2. Suppose there exists a nonzero additive mapping D:R → R satisfying the relation D(xm+n+1)=(m+n+1)xmD(x)xn for all x 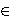 R. In this case D is a derivation and R
is commutative.
R. In this case D is a derivation and R
is commutative.
2000 Mathematics Subject Classification.
16N60, 39B05.
Key words and phrases. Prime ring, functional identity, derivation.
Full text (PDF) (free access)
DOI: 10.3336/gm.46.1.06
References:
- K. I. Beidar, M. Brešar and M. A. Chebotar, Functional identities revised: the fractional and the strong degree, Comm. Algebra 30 (2002), 935-969.
MathSciNet
CrossRef
- K. I. Beidar and M. A. Chebotar, On functional identities and d-free subsets of rings I, Comm. Algebra 28 (2000), 3925-3951.
MathSciNet
CrossRef
- K. I. Beidar and Y. Fong, On additive isomorphisms of prime rings preserving polynomials, J. Algebra 217 (1999), 650-667.
MathSciNet
CrossRef
- K. I. Beidar, W. S. Martindale, III and A. V. Mikhalev, Rings with generalized identities, Marcel Dekker, Inc., New York, 1996.
MathSciNet
- K. I. Beidar, A. V. Mikhalev and M. A. Chebotar, Functional identities in rings and their applications, Russian Math. Surveys 59 (2004), 403-428.
MathSciNet
CrossRef
- M. Brešar, A generalization of the notion of centralizing mappings, Proc.
Amer. Math. Soc. 114 (1992), 641-649.
MathSciNet
CrossRef
- M. Brešar, Functional identities: A survey, Contemp. Math.
259 (2000), 93-109.
MathSciNet
- M. Brešar and J. Vukman, On left derivations and related mappings, Proc.
Amer. Math. Soc. 110 (1990), 7-16.
MathSciNet
CrossRef
- Q. Deng, On Jordan left derivations, Math. J. Okayama Univ. 34
(1992), 145-147.
MathSciNet
- E. C. Posner, Derivations in prime rings, Proc. Amer. Math. Soc. 8
(1957), 1093-1100.
MathSciNet
CrossRef
- L. H. Rowen, Some results on the center of a ring with polynomial identity,
Bull. Amer. Math. Soc. 79 (1973), 219-223.
MathSciNet
CrossRef
- J. Vukman, Commuting and centralizing mappings in prime rings Proc. Amer. Math. Soc. 109
(1990), 47-52.
MathSciNet
CrossRef
- J. Vukman, On left Jordan derivations of rings and
Banach algebras, Aequationes Math. 75 (2008), 260-266.
MathSciNet
CrossRef
- J. Vukman and M. Fošner, A characterization of two-sided centralizers on prime rings, Taiwanese J. Math. 11 (2007), 1431-1441.
MathSciNet
- J. Vukman and I. Kosi-Ulbl, On some equations related to
derivations in rings, Internat. J. Math. Math. Sci. 17 (2005), 2703-2710.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
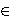 R. In this case D is a derivation and R
is commutative.
R. In this case D is a derivation and R
is commutative.
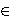 R. In this case D is a derivation and R
is commutative.
R. In this case D is a derivation and R
is commutative.