Glasnik Matematicki, Vol. 45, No.2 (2010), 513-523.
CONVERGENCE THEOREMS OF ZEROS OF A FINITE FAMILY OF m-ACCRETIVE OPERATORS IN BANACH SPACES
Yan Hao and Sun Young Cho
School of Mathematics, Physics and Information
Science, Zhejiang Ocean University, Zhoushan 316004, China
e-mail: zjhaoyan@yahoo.cn
Department of Mathematics, Gyeongsang National University, Chinju 660-701, Korea
e-mail: ooly61@yahoo.co.kr
Abstract. In this paper, we continue to study convergence problems
for a Ishikawa-like iterative process for a finite family of
m-accretive mappings. Strong convergence theorems are established
in uniformly smooth Banach spaces.
2000 Mathematics Subject Classification.
47H09, 47J25.
Key words and phrases. Accretive mapping, pseudo-contractive mapping, iterative process, zero.
Full text (PDF) (free access)
DOI: 10.3336/gm.45.2.16
References:
- F. E. Browder, Fixed point theorems for noncompact mappings in Hilbert space, Proc. Nat. Acad. Sci. USA 53 (1965), 1272-1276.
MathSciNet
- V. Berinde, Iterative approximation of fixed points, Editura
Efemeride, Baia Mare, 2002.
MathSciNet
- R. E. Bruck Jr., A strongly convergent iterative solution of 0
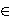 U(x) for a maximal monotone operator U in Hilbert space, J. Math. Anal.
Appl. 48 (1974), 114-126.
U(x) for a maximal monotone operator U in Hilbert space, J. Math. Anal.
Appl. 48 (1974), 114-126.
MathSciNet
CrossRef
- R. E. Bruck, Nonexpansive projections on subsets of Banach spaces, Pacific J. Math. 47 (1973), 341-355.
MathSciNet
CrossRef
- C. E. Chidume and H. Zegeye, Iterative solution of 0
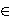 Ax for m-accretive operator A in certain Banach spaces, J. Math. Anal. Appl. 269 (2002), 421-430.
Ax for m-accretive operator A in certain Banach spaces, J. Math. Anal. Appl. 269 (2002), 421-430.
MathSciNet
CrossRef
- Y. J. Cho and X. Qin, Viscosity approximation methods for a family of m-accretive mappings in reflexive Banach spaces,
Positivity 12 (2008), 483-494.
MathSciNet
CrossRef
- Y. J. Cho and X. Qin, Convergence of a general iterative method for nonexpansive mappings in Hilbert spaces, J. Comput. Appl. Math. 228 (2009), 458-465.
MathSciNet
CrossRef
- Y. J. Cho, S. M. Kang and X. Qin, Approximation of common fixed points of an infinite family of nonexpansive mappings in Banach spaces, Comput. Math. Appl. 56 (2008), 2058-2064.
MathSciNet
CrossRef
- L. C. Ceng, A. R. Khan, Q. H. Ansari and J.-C. Yao, Strong convergence of composite iterative schemes for zeros of m-accretive operators in Banach spaces, Nonlinear Anal. 70 (2009), 1830-1840.
MathSciNet
CrossRef
- T. Dominguez Benavides, G. Lobez Acedo and H.-K. Xu, Iterative solutions for zeros of accretive operators, Math. Nachr.
248/249 (2003), 62-71.
MathSciNet
CrossRef
- J. S. Jung, Convergence of composite iterative methods for finding zeros of accretive operators, Nonlinear Anal. 71 (2009), 1736-1746.
MathSciNet
CrossRef
- T. H. Kim and H. K. Xu, Strong convergence of modified Mann iterations, Nonlinear Appl. 61 (2005),
51-60.
MathSciNet
CrossRef
- W. R. Mann, Mean value methods in iteration, Proc. Amer.
Math. Soc. 4 (1953), 506-510.
MathSciNet
CrossRef
- X. Qin, Y. J. Cho, J. I. Kang and S. M. Kang, Strong convergence theorems for an infinite family of nonexpansive mappings in Banach spaces, J. Comput. Appl. Math. 230 (2009), 121-127.
MathSciNet
CrossRef
- X. Qin and Y. Su, Approximation of zero point of accretive operator in Banach spaces, J. Math. Anal. Appl.
329 (2007), 415-424.
MathSciNet
CrossRef
- X. Qin, Y. Su and M. Shang, Strong convergence of the composite Halpern iteration, J. Math. Anal. Appl. 339 (2008), 996-1002.
MathSciNet
CrossRef
- X. Qin and Y. Su, Strong convergence theorems for relatively nonexpansive mappings in a Banach space, Nonlinear Anal. 67 (2007), 1958-1965.
MathSciNet
CrossRef
- S. Reich, Weak convergence theorems for nonexpansive mappings in Banach spaces, J. Math. Anal. Appl. 67
(1979), 274-276.
MathSciNet
CrossRef
- S. Reich, Strong convergence theorems for resolvents of accretive operators in Banach spaces, J. Math. Anal. Appl.
75 (1980), 287-292.
MathSciNet
CrossRef
- S. Reich, Asymptotic behavior of contractions in Banach spaces, J. Math. Anal. Appl. 44 (1973), 57-70.
MathSciNet
CrossRef
- T. Suzuki, Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals, J. Math. Anal. Appl.
305 (2005), 227-239.
MathSciNet
CrossRef
- M. Shang, Y. Su and X. Qin, Strong convergence theorems for a finite family of nonexpansive mappings, Fixed Point Theory Appl. 2007 (2007), Art. ID
76971, 9pp.
MathSciNet
- W. Takahashi, Nonlinear Functional Analysis,
Yokohama Publishers, Yokohama, 2000.
MathSciNet
- H. K. Xu, Iterative algorithms for nonlinear operators, J. London Math. Soc. (2) 66 (2002),
240-256.
MathSciNet
CrossRef
- Y. Yao, R. Chen and J. C. Yao, Strong convergence and certain control conditions for modified Mann iteration, Nonlinear Anal. 68 (2008), 1687-1693.
MathSciNet
- H. Zegeyea and N. Shahzad, Strong convergence theorems for a common zero of a finite family of m-accretive mappings, Nonlinear Anal.
66 (2007), 1161-1169.
MathSciNet
CrossRef
- E. Zeidler, Nonlinear functional analysis and its applications, Part II: Monotone Operators, Springer-Verlag,
Berlin, 1985.
Glasnik Matematicki Home Page
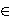 U(x) for a maximal monotone operator U in Hilbert space, J. Math. Anal.
Appl. 48 (1974), 114-126.
U(x) for a maximal monotone operator U in Hilbert space, J. Math. Anal.
Appl. 48 (1974), 114-126.
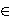 Ax for m-accretive operator A in certain Banach spaces, J. Math. Anal. Appl. 269 (2002), 421-430.
Ax for m-accretive operator A in certain Banach spaces, J. Math. Anal. Appl. 269 (2002), 421-430.