Glasnik Matematicki, Vol. 45, No.2 (2010), 453-460.
DIRAC COHOMOLOGY AND THE BOTTOM LAYER K-TYPES
Pavle Pandžić
Department of Mathematics, University of Zagreb, Bijenička 30,
10 000 Zagreb, Croatia
e-mail: pandzic@math.hr
Abstract. Let G be a connected real reductive Lie group with a maximal compact subgroup K corresponding to a Cartan involution Θ of G. Let q=l 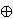 u be a θ-stable parabolic subalgebra of the complexified Lie algebra g of G, where θ=dΘ. Let L be the centralizer of q in G.
We show that, under certain dominance assumptions, cohomological induction with respect to q takes irreducible unitary (l,L ∩ K)-modules with nonzero Dirac cohomology to irreducible unitary (g,K)-modules which also have nonzero Dirac cohomology.
u be a θ-stable parabolic subalgebra of the complexified Lie algebra g of G, where θ=dΘ. Let L be the centralizer of q in G.
We show that, under certain dominance assumptions, cohomological induction with respect to q takes irreducible unitary (l,L ∩ K)-modules with nonzero Dirac cohomology to irreducible unitary (g,K)-modules which also have nonzero Dirac cohomology.
2000 Mathematics Subject Classification.
22E47.
Key words and phrases. Reductive Lie group, unitary representation, Harish-Chandra module, Dirac operator, Dirac cohomology, cohomological induction, bottom layer.
Full text (PDF) (free access)
DOI: 10.3336/gm.45.2.12
References:
- C. Chevalley, The algebraic theory of spinors, Columbia University Press, 1954.
MathSciNet
- T. J. Enright, R. Howe and N. R. Wallach, A classification of unitary highest weight modules, in Representation theory of reductive groups, Park City, Utah,
1982, Birkhäuser, Boston, 1983, 97-143.
MathSciNet
- J.-S. Huang, Y.-F. Kang and P. Pandžić, Dirac cohomology of some Harish-Chandra modules, Transform. Groups 14 (2009), 163-173.
MathSciNet
CrossRef
- J.-S. Huang and P. Pandžić, Dirac cohomology, unitary representations and a proof of a conjecture of Vogan, J. Amer. Math. Soc. 15 (2002), 185-202.
MathSciNet
CrossRef
- J.-S. Huang and P. Pandžić,
Dirac operators in representation theory, Mathematics: Theory and Applications, Birkhauser, 2006.
MathSciNet
- J.-S. Huang, P. Pandžić and V. Protsak,
Dirac cohomology of Wallach representations, preprint, 2009.
- J.-S. Huang, P. Pandžić and D. Renard,
Dirac operators and Lie algebra cohomology, Represent. Theory 10 (2006), 299-313.
MathSciNet
CrossRef
- A. W. Knapp and D. A. Vogan, Cohomological induction and unitary representations, Princeton University Press, 1995.
MathSciNet
- B. Kostant,
Clifford algebra analogue of the Hopf-Koszul-Samelson theorem, the ρ-decomposition C(g)=End Vρ⊗ C(P), and the g-module structure of ⋀ g,
Adv. Math. 125 (1997), no. 2, 275-350.
MathSciNet
CrossRef
- B. Kostant,
A cubic Dirac operator and the emergence of Euler number multiplets of representations for equal rank subgroups,
Duke Math. J. 100 (1999), 447-501.
MathSciNet
CrossRef
- R. Parthasarathy,
Dirac operator and the discrete series,
Ann. of Math. 96 (1972), 1-30.
MathSciNet
CrossRef
- K. R. Parthasarathy, R. Ranga Rao and V. S. Varadarajan, Representations of complex semisimple Lie groups and Lie algebras, Ann. of Math. 85 (1967), 383-429.
MathSciNet
CrossRef
- D. A. Vogan,
Representations of real reductive Lie groups, Birkhäuser,
Boston, 1981.
MathSciNet
- D. A. Vogan, Dirac operators and unitary representations,
3 talks at MIT Lie groups seminar, Fall 1997.
- D. A. Vogan, G. J. Zuckerman,
Unitary representations with non-zero cohomology, Compositio Math. 53 (1984), 51-90.
MathSciNet
CrossRef
- N. R. Wallach,
Real Reductive Groups, Volume I,
Academic Press, 1988.
MathSciNet
Glasnik Matematicki Home Page
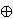 u be a θ-stable parabolic subalgebra of the complexified Lie algebra g of G, where θ=dΘ. Let L be the centralizer of q in G.
We show that, under certain dominance assumptions, cohomological induction with respect to q takes irreducible unitary (l,L ∩ K)-modules with nonzero Dirac cohomology to irreducible unitary (g,K)-modules which also have nonzero Dirac cohomology.
u be a θ-stable parabolic subalgebra of the complexified Lie algebra g of G, where θ=dΘ. Let L be the centralizer of q in G.
We show that, under certain dominance assumptions, cohomological induction with respect to q takes irreducible unitary (l,L ∩ K)-modules with nonzero Dirac cohomology to irreducible unitary (g,K)-modules which also have nonzero Dirac cohomology.