Glasnik Matematicki, Vol. 45, No.1 (2010), 173-217.
ON EXPANSIONS AND PRO-PRO-CATEGORIES
Nikica Uglešić and Vlasta Matijević
University of Zadar, Pavlinovićeva bb, 23000 Zadar, Croatia
e-mail: nuglesic@unizd.hr
Department of Mathematics, University of Split, Teslina 12/III, 21000 Split, Croatia
e-mail: vlasta@pmfst.hr
Abstract. If
(C,D)
is a category pair such that
D
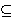 C
is a pro-reflective subcategory, then so is
D
C
is a pro-reflective subcategory, then so is
D
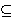 pro-C
and, inductively, D
pro-C
and, inductively, D
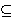 pronC
as well. The key fact is that the terms and
morphisms of D-expansions of
all the terms of a C-system
can be naturally organized in a D-expansion of the
system. Therefore, in dealing with expansions, there is no need to involve the
pro-pro-category technique. In particular, the shape of a
C-system,
as well as of a C-object,
reduces to the isomorphism
class of a D-system.
On the other hand, a pro-pro-category could
be useful for some other purposes because it admits functorial expansions
which are inverse limits. Some applications of the theoretical part are
considered, especially, concerning the Stone-Čech compactification and
Hewitt realcompactification.
pronC
as well. The key fact is that the terms and
morphisms of D-expansions of
all the terms of a C-system
can be naturally organized in a D-expansion of the
system. Therefore, in dealing with expansions, there is no need to involve the
pro-pro-category technique. In particular, the shape of a
C-system,
as well as of a C-object,
reduces to the isomorphism
class of a D-system.
On the other hand, a pro-pro-category could
be useful for some other purposes because it admits functorial expansions
which are inverse limits. Some applications of the theoretical part are
considered, especially, concerning the Stone-Čech compactification and
Hewitt realcompactification.
2000 Mathematics Subject Classification.
55P55, 18A32.
Key words and phrases. Pro-category, pro-pro-category, expansion, pro-reflective subcategory, shape,
polyhedron, compact Hausdorff space, completely regular space, Stone-Čech
compactification, Hewitt realcompactification.
Full text (PDF) (free access)
DOI: 10.3336/gm.45.1.13
References:
- M. Artin and B. Mazur,
Etale Homotopy, Lecture Notes in
Mathematics 100, Springer-Verlag, Berlin - Heidelberg, 1969.
MathSciNet
- J. Dugundji,
Topology, Allyn and Bacon, Boston, 1978.
MathSciNet
- Encyclopedia of General Topology,
K. P. Hart, J. Nagata and J. E. Vaughan (editors), Elsevier, North-Holland, Amsterdam, 2004.
MathSciNet
- I. Glicksberg,
The Stone - Čech compactification of
products, Trans. Amer. Math. Soc. 90 (1959), 369-382.
MathSciNet
CrossRef
- L. Gillman and M. Jerison,
Rings of continuous
functions, Grad. Texts in Math. 43, Springer Verlag, 1976.
MathSciNet
- W. Holsztynsky,
An extension and axiomatic
characterization of Borsuk's theory of shape, Fund. Math. 70 (1971), 157-168.
MathSciNet
- R. D. Kopperman and R. G. Wilson,
Finite approximation
of compact Hausdorff spaces, Topology Proc. 22 (1977), 175-200.
MathSciNet
- V. A. Kovalevsky,
Finite topology as applied to image
analysis, Comput. Vision Graphics Image Process. 46 (1989), 141-161.
CrossRef
- S. Mardesic,
Shape theory,
Proceedings of the International Congress of Mathematicians (Helsinki, 1978), (1980), 481-489.
MathSciNet
- S. Mardesic and J. Segal,
Shapes of compacta
and ANR-systems, Fund. Math. 72 (1971), 41-59.
MathSciNet
- S. Mardesic and J. Segal,
Shape Theory,
North-Holland, Amsterdam, 1982.
MathSciNet
- S. Mardesic and N. Uglesic,
On iterated
inverse limits. In memory of T. Benny Rushing, Topology Appl. 120 (2002), 157-167.
MathSciNet
CrossRef
- K. Morita,
The Hurewicz and the Whitehead theorems in
shape theory, Sci. Rep. Tokyo Kyoiku Daigaku Sect. A 12 (1974), 246-258.
MathSciNet
- K. Morita,
On shapes of topological spaces, Fund. Math.
86 (1975), 251-259.
MathSciNet
- L. Stramaccia,
Reflective subcategories and dense
subcategories, Rend. Sem. Mat. Univ. Padova 67 (1982), 191-198.
MathSciNet
Numdam
- W. Tholen,
Pro-categories and multiadjoint functors, Canad. J. Math. 36 (1984), 144-155.
MathSciNet
- N. Uglesic,
Iterated resolutions, Glas. Mat. Ser. III
35(55) (2000), 245-259.
MathSciNet
- M. D. Weir,
Hewitt-Nachbin spaces, North-Holland,
Amsterdam, 1975.
MathSciNet
Glasnik Matematicki Home Page
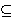 C
C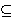 pro-C
pro-C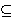 pronC
pronC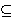 C
C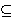 pro-C
pro-C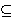 pronC
pronC