Glasnik Matematicki, Vol. 44, No.2 (2009), 457-478.
COMPACTIFICATIONS OF [0,∞) WITH UNIQUE
HYPERSPACE Fn(X)
Alejandro Illanes and Jorge M. Martinez-Montejano
Universidad Nacional Autónoma de México,
Instituto de Matemáticas, Circuito Exterior, Cd. Universitaria, México, 04510,
D.F. Mexico
e-mail: illanes@matem.unam.mx
e-mail: jorge@matem.unam.mx
Abstract. Given a metric continuum X,
Fn(X) denotes the hyperspace of nonempty
subsets of X with at most n elements. In this paper we show the
following result. Suppose that X is a metric compactification of
[0,∞), Y is a continuum and Fn(X)
is homemorphic to Fn(Y).
Then: (a) if n ≠ 3, then X is homeomorphic to Y, (b) if n = 3 and
the remainder of X is an ANR, then X is homeomorphic to Y. The
question if the result in (a) is valid for n = 3 remains open.
2000 Mathematics Subject Classification.
54B20,54F15.
Key words and phrases. Compactification, continuum, hyperspace,
ray, symmetric product, unique hyperspace.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.2.12
References:
- G. Acosta, R. Hernández-Gutiérrez and V. Martinez-de-la-Vega,
Dendrites and symmetric products,
Glas. Mat. Ser. III 44(64) (2009), 195-210.
MathSciNet
CrossRef
- R. Bott,
On the third symmetric potency of S1, Fund. Math.
39 (1952), 264-268.
MathSciNet
- E. Castaneda and A. Illanes,
Finite graphs have unique
symmetric products, Topology Appl. 153 (2006), 1434-1450.
MathSciNet
CrossRef
- J. J. Charatonik and A. Illanes,
Local Connectedness in
Hyperspaces, Rocky Mountain J. Math. 36 (2006), 811-856.
MathSciNet
CrossRef
- D. W. Curtis and N. T. Nhu,
Hyperspaces of finite sets which are
homemomorphic to
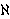 0-dimensional linear metric spaces,
Topology Appl. 19 (1985), 251-260.
0-dimensional linear metric spaces,
Topology Appl. 19 (1985), 251-260.
MathSciNet
CrossRef
- V. Guillemin and A. Pollack,
Differential Topology,
Prentice-Hall, Inc., Englewood Cliff, 1974.
MathSciNet
- D. Herrera-Carrasco, M. de J. López and F. Macias-Romero,
Dendrites with unique symmetric products, Topology Proc. 34 (2009), 175-190.
- A. Illanes,
Dendrites with unique hyperspace C2(X), II,
Topology Proc. 34 (2009), 77-96.
MathSciNet
- A. Illanes and S. B. Nadler, Jr.,
Hyperspaces. Fundamentals and
recent advances, Monographs and Textbooks in Pure and Applied Mathematics 216,
Marcel Dekker, Inc., New York, 1999.
MathSciNet
- S. B. Nadler, Jr.,
Hyperspaces of sets. A text with research
questions, Monographs and Textbooks in Pure and Applied Mathematics, vol.
49, Marcel Dekker, Inc., New York-Basel, 1978.
MathSciNet
- E. H. Spanier,
Algebraic Topology, McGraw-Hill Book Co., New York-Toronto-London, 1966.
MathSciNet
Glasnik Matematicki Home Page
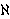 0-dimensional linear metric spaces,
Topology Appl. 19 (1985), 251-260.
0-dimensional linear metric spaces,
Topology Appl. 19 (1985), 251-260.