Glasnik Matematicki, Vol. 44, No.2 (2009), 401-421.
A RESULT IN ASYMPTOTIC ANALYSIS FOR THE
FUNCTIONAL OF GINZBURG-LANDAU TYPE WITH
EXTERNALLY IMPOSED MULTIPLE SMALL SCALES IN ONE DIMENSION
Andrija Raguž
Department of Mathematics, University of Zagreb, 10 000 Zagreb, Croatia
e-mail: andrija@math.hr
Abstract. In this paper we present technical improvement of
results in our previous paper. We study asymptotic behavior of the
functional
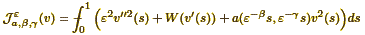
as ε → 0, where a is 1 × 1-periodic. We determine
(rescaled) minimal asymptotic energy associated to
Jεa,β,γ as
ε → 0 where β, γ ≥ 0, β + γ > 0.
2000 Mathematics Subject Classification.
34E15, 49J45.
Key words and phrases. Minimization, multiple small scales, Ginzburg-Landau
functional, Gamma convergence.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.2.09
References:
- G. Alberti and S. Müller,
A new approach to
variational problems with multiple scales, Comm. Pure Appl.
Math. 54 (2001), 761-825.
MathSciNet
CrossRef
- R. Choksi,
Scaling laws in microphase
separation of diblock copolymers, J. Nonlinear Sci.
11 (2001), 223-236.
MathSciNet
CrossRef
- G. DalMaso,
An Introduction to Γ-convergence,
Progress in Nonlinear Differential Equations and their Applications, 8.
Birkhäuser Boston, Inc., Boston, 1993.
MathSciNet
- N. Dirr, M. Lucia and M. Novaga,
Γ-convergence of the Allen-Cahn energy
with an oscillation forcing term, Interfaces Free Bound. 8 (2006), 47-78.
MathSciNet
- L. C. Evans and R. F. Gariepy,
Measure theory and fine properties of functions, CRC Press, Boca Raton, 1992.
MathSciNet
- I. Fonseca,
Phase transitions of
elastic solid materials, Arch. Rational Mech. Anal. 107
(1989), 195-223.
MathSciNet
CrossRef
- I. Fonseca and L. Tartar,
The gradient theory
of phase transitions for systems with two potential wells,
Proc. Roy. Soc. Edinburgh Sect. A 111 (1989), 89-102.
MathSciNet
- A. Khachaturyan,
Theory of structural
transformations in solids, New York, John Wiley and Sons 1983.
- A. Khachaturyan,
Some questions concerning the
theory of phase transformations in solids, Sov. Phys. - Solid
State 8 (1967), 2163-2168.
- A. Khachaturyan and G. Shatalov,
Theory of
macroscopic periodicity for a phase transition in a solid state,
Sov. Phys. JETP 29 (1969), 557-561.
- R. V. Kohn and S. Müller,
Branching of twins near an
austensite-twinned-martensite interface, Philosophical Magazine
A 66 (1992), 697-715.
CrossRef
- R. V. Kohn and S. Müller,
Surface energy
and microstructure in coherent phase transitions,
Comm. Pure
Appl. Math. 47 (1994), 405-435.
MathSciNet
MathSciNet
- S. Müller,
Singular perturbations
as a selection criterion for minimizing sequences,
Calc. Var. Partial Differential Equations 1 (1993), 169-204.
MathSciNet
CrossRef
- T. Ohta and K. Kawasaki,
Equilibrium morphology of block
copolymer melts, Macromolecules 19 (1986), 2621-2632.
CrossRef
- A. Raguz,
On some questions related to relaxation
and minimization for a class of functionals of Ginzburg-Landau type
in one dimension, PhD Thesis, University of Zagreb 2004,
http://web.math.hr/~andrija/doktorat5.pdf (in Croatian).
- A. Raguz,
Relaxation of Ginzburg-Landau
functional with 1-Lipschitz penalizing term in one dimension by
Young measures on micro-patterns,
Asymptotic Anal. 41 (2005), 331-361.
MathSciNet
- A. Raguz,
Computation of
Ginzburg-Landau energy with nonlinear term, submitted.
- A. Raguz,
A note on calculation of asymptotic energy for a
functional of Ginzburg-Landau type with externally imposed
lower-order oscillatory term in one dimension,
Boll. Unione Mat. Ital. Sez. B Artic. Ric. Mat. (8) 10 (2007), 1125-1142.
MathSciNet
- C. I. Zeppieri,
Multi-scale analysis via
Γ-convergence, PhD Thesis, Universitá degli Studi di Roma
"La Sapienza", 2006, http://cvgmt.sns.it/papers/zep06/.
Glasnik Matematicki Home Page