Glasnik Matematicki, Vol. 44, No.2 (2009), 343-348.
ON AUTOMORPHISMS OF ORDER p OF METACYCLIC
p-GROUPS WITHOUT CYCLIC SUBGROUPS OF INDEX p
Yakov Berkovich
Department of Mathematics, University of Haifa, Mount Carmel, Haifa 31905, Israel
e-mail: berkov@math.haifa.ac.il
Abstract. Let L be a metacyclic p-group, p > 2, without
cyclic subgroups of index p and let
a 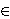 Aut(L)
be of order
p. We show that either a centralizes
Ω1(L) or p = 3 and
the natural semidirect product < a > · L is of maximal class so the subgroup
L has very specific structure.
This improves a result by Meierfrankenfeld and Stellmacher.
Aut(L)
be of order
p. We show that either a centralizes
Ω1(L) or p = 3 and
the natural semidirect product < a > · L is of maximal class so the subgroup
L has very specific structure.
This improves a result by Meierfrankenfeld and Stellmacher.
2000 Mathematics Subject Classification.
20D15.
Key words and phrases. Metacyclic, minimal nonmetacyclic and minimal nonabelian p-groups,
p-groups of maximal class.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.2.07
References:
- M. Aschbacher and S. D. Smith,
The classification of quasithin groups. I. Structure of strongly
quasithin K-groups, Mathematical Surveys and Monographs 111.
American Mathematical Society, Providence, RI, 2004.
MathSciNet
- Y. Berkovich,
On subgroups of finite p-groups, J. Algebra
224 (2000), 198-240.
MathSciNet
CrossRef
- Y. Berkovich,
Groups of prime power order. Vol. 1. With a foreword by Zvonimir Janko,
de Gruyter Expositions in Mathematics 46, Walter de Gruyter GmbH & Co. KG, Berlin, 2008.
MathSciNet
- Y. Berkovich,
On subgroups and epimorphic images of finite
p-groups, J. Algebra 248 (2002), 472-553.
MathSciNet
CrossRef
- Y. Berkovich,
On abelian subgroups of p-groups,
J. Algebra 199 (1998), 262-280.
MathSciNet
CrossRef
- Y. Berkovich,
Short proofs of some basic characterization
theorems of finite p-group theory,
Glas. Mat. Ser. III 41(61) (2006),
239-258.
MathSciNet
CrossRef
- Y. Berkovich and Z. Janko,
Structure of finite p-groups with
given subgroups, Contemp. Math. 402 (2006), 13-93.
MathSciNet
- B. Huppert,
Endliche Gruppen. I, Springer-Verlag, Berlin-New York, 1967.
MathSciNet
- I. Isaacs,
Algebra. A graduate course, Brooks/Cole Publishing Co., Pacific Grove, CA, 1994.
MathSciNet
- Z. Janko,
Finite 2-groups with exactly four cyclic subgroups
of order 2n, J. Reine Angew. Math. 566 (2004), 135-181.
MathSciNet
CrossRef
- U. Meierfrankenfeld and B. Stellmacher,
The generic groups of
p-type, preprint, Michigan State University, 1997.
- L. Redei,
Das "schiefe Produkt" in der Gruppentheorie mit
Anwendung auf die endlichen nichtkommutativen Gruppen mit lauter
kommutativen echten Untergruppen und die Ordnungzahlen, zu denen nur
kommutative Gruppen gehören, Comment. Math. Helv. 20
(1947), 225-264.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
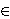 Aut(L)
Aut(L)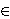 Aut(L)
Aut(L)