Glasnik Matematicki, Vol. 44, No.2 (2009), 323-331.
ON THE APPROXIMATION TO ALGEBRAIC NUMBERS
BY ALGEBRAIC NUMBERS
Yann Bugeaud
Université de Strasbourg, U. F. R. de mathématiques,
7, rue René Descartes, 67084 Strasbourg Cedex, France
e-mail: bugeaud@math.u-strasbg.fr
Abstract. Let n be a positive integer.
Let ξ be an algebraic real number of degree greater than n.
It follows from a deep
result of W. M. Schmidt that,
for every positive real number ε,
there are infinitely many algebraic numbers α
of degree at most n such that
|ξ - α| < H(α)-n - 1 + ε,
where H(α) denotes the
naive height of α. We sharpen this result by replacing
ε by a function H 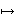 ε(H)
that tends to zero when H
tends to infinity. We make a similar improvement for the approximation
to algebraic numbers by algebraic integers, as well as for an
inhomogeneous approximation problem.
ε(H)
that tends to zero when H
tends to infinity. We make a similar improvement for the approximation
to algebraic numbers by algebraic integers, as well as for an
inhomogeneous approximation problem.
2000 Mathematics Subject Classification.
11J68.
Key words and phrases. Approximation by algebraic numbers, Schmidt Subspace Theorem.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.2.05
References:
- Y. Bugeaud,
Approximation by algebraic integers and Hausdorff dimension,
J. London Math. Soc. (2) 65 (2002), 547-559.
MathSciNet
CrossRef
- Y. Bugeaud,
Approximation by algebraic numbers,
Cambridge Tracts in Mathematics 160, Cambridge University Press, Cambridge, 2004.
MathSciNet
-
Y. Bugeaud,
Extensions of the Cugiani-Mahler Theorem,
Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 6 (2007), 477-498.
MathSciNet
- Y. Bugeaud and M. Laurent,
Exponents of homogeneous and inhomogeneous Diophantine
Approximation,
Mosc. Math. J. 5 (2005), 747-766.
MathSciNet
- Y. Bugeaud et O. Teulié,
Approximation d'un nombre réel par des nombres
algébriques de degré donné,
Acta Arith. 93 (2000), 77-86.
MathSciNet
- J. W. S. Cassels,
An introduction to Diophantine approximation,
Cambridge Tracts in Mathematics and Mathematical Physics, No. 45, Cambridge
University Press, New York, 1957.
MathSciNet
- M. Cugiani,
Sull'approssimazione di numeri algebrici mediante razionali,
Collectanea Mathematica,
Pubblicazioni dell'Istituto di matematica dell'Universitá di Milano 169,
Ed. C. Tanburini, Milano,
pagg. 5 (1958).
- H. Davenport and W. M. Schmidt,
Approximation to real numbers
by quadratic irrationals, Acta Arith. 13 (1967/1968), 169-176.
MathSciNet
- H. Davenport and W. M. Schmidt,
Approximation to real numbers by
algebraic integers, Acta Arith. 15 (1968/1969), 393-416.
MathSciNet
- J.-H. Evertse and H.P. Schlickewei,
A quantitative version of the absolute subspace theorem,
J. Reine Angew. Math. 548 (2002), 21-127.
MathSciNet
CrossRef
- D. Kleinbock and B. Weiss,
Dirichlet's theorem on Diophantine approximation and homogeneous flows,
J. Mod. Dyn. 2 (2008), 43-62.
MathSciNet
- K. Mahler,
Lectures on Diophantine approximation,
Part 1: g-adic numbers and Roth's theorem,
University of Notre Dame Press, Notre Dame, Ind 1961.
MathSciNet
- K. Mahler,
On the approximation of algebraic numbers by algebraic integers,
J. Austral. Math. Soc. 3 (1963), 408-434.
MathSciNet
CrossRef
- K. F. Roth,
Rational approximations to algebraic numbers,
Mathematika 2 (1955), 1-20; corrigendum, 168.
MathSciNet
- W. M. Schmidt,
Simultaneous approximations to algebraic numbers by rationals,
Acta Math. 125 (1970), 189-201.
MathSciNet
CrossRef
- W. M. Schmidt,
Approximation to algebraic numbers,
Enseignement Math. (2) 17 (1971), 187-253.
MathSciNet
- W. M. Schmidt,
Diophantine approximation, Lecture Notes in Math.
785, Springer, Berlin, 1980.
MathSciNet
- W. M. Schmidt,
The subspace theorem in Diophantine approximation,
Compositio Math. 69 (1989), 121-173.
MathSciNet
- O. Teulié,
Approximation d'un nombre r\'eel par des unités algébriques,
Monatsh. Math. 132 (2001), 169-176.
MathSciNet
CrossRef
- E. Wirsing,
Approximation mit algebraischen Zahlen beschränkten Grades,
J. Reine Angew. Math. 206 (1961), 67-77.
MathSciNet
Glasnik Matematicki Home Page
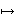 ε(H)
ε(H)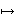 ε(H)
ε(H)