Glasnik Matematicki, Vol. 44, No.2 (2009), 285-307.
ARITHMETIC PROPERTIES OF THE INTEGER PART OF
THE POWERS OF AN ALGEBRAIC NUMBER
Florian Luca and Maurice Mignotte
Instituto de Matemáticas, Universidad Nacional Autónoma de México,
C.P. 58089, Morelia, Michoacán, México
e-mail: fluca@matmor.unam.mx
Université Louis Pasteur, UFR de mathématiques,
7 rue René Descartes, 67084 Strasbourg, France
e-mail: mignotte@math.u-strasbg.fr
Abstract. For a real number x, we let
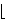 x
x![]](symbol/rceil.gif) be the closest integer to
x. In
this paper, we look at the arithmetic properties of the integers
be the closest integer to
x. In
this paper, we look at the arithmetic properties of the integers
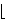 θn
θn![]](symbol/rceil.gif) when n ≥ 0, where θ > 1 is a fixed
algebraic number.
when n ≥ 0, where θ > 1 is a fixed
algebraic number.
2000 Mathematics Subject Classification.
11D45, 11D75.
Key words and phrases. Powers of algebraic numbers, digital representations,
applications of linear forms in logarithms and the subspace theorem.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.2.03
References:
- P. Corvaja and U. Zannier,
Some new applications of the subspace theorem,
Compositio Math. 131 (2002), 319-340.
MathSciNet
CrossRef
- G. Everest, A. van der Poorten, I. Shparlinski and T. Ward,
Recurrence sequences, Mathematical Surveys and Monographs 104,
American Mathematical Society, Providence, 2003.
MathSciNet
- J.-H. Evertse,
On sums of S-units and linear recurrences,
Compositio Math. 53 (1984), 225-244.
MathSciNet
- J.-H. ~Evertse,
An improvement of the quantitative subspace
theorem, Compositio Math. 101 (1996), 225-311.
MathSciNet
- C. Fuchs,
Polynomial-exponential
equations and linear recurrences, Glas.
Mat. Ser. III 38(58) (2003), 233-252.
MathSciNet
- C. Fuchs,
Polynomial-exponential equations involving multirecurrences,
Studia Sci. Math. Hungar. 46} (2009), 377-398.
- C. Fuchs and A. Scremin,
Polynomial-exponential equations involving several
linear recurrences, Publ. Math. Debrecen 65 (2004), 149-172.
MathSciNet
- F. Luca,
Distinct digits in base $b$ expansions of linear
recurrence sequences, Quaest. Math. 23 (2000), 389-404.
MathSciNet
- F. Luca,
Arithmetic properties of positive integers with
fixed digit sum, Rev. Mat. Iberoam. 22 (2006), 369-412.
MathSciNet
- E. M. Matveev,
An explicit lower bound for a
homogeneous rational linear form in logarithms of algebraic numbers. II,
Izv. Ross. Akad. Nauk Ser. Mat. 64 (2000), 125-180.
English transl. in Izv. Math. 64 (2000), 1217-1269.
MathSciNet
CrossRef
- M. Mignotte,
Sur les conjugués des nombres de Pisot,
C. R. Acad. Sci. Paris Sér. I Math. 298 (1984), 21.
MathSciNet
- A. J. van der Poorten,
Some facts that should be
better known especially about rational functions, in: Number
Theory and its Applications, R. A. Mollin (Ed.), Kluwer Acad. Publ., Dordrecht, 1989, 497-528.
MathSciNet
- A. J. van der Poorten and H. P. Schlickewei,
Additive relations in fields,
J. Austral. Math. Soc. Ser. A 51 (1991), 154-170.
MathSciNet
- J. F. Ritt,
A factorization theory for functions
∑i=1n aieαiz,
Trans. Amer. Math. Soc. 29 (1927), 584-596.
MathSciNet
CrossRef
- T. N. Shorey and C. L. Stewart,
Pure powers in recurrence
sequences and some related Diophantine equations,
J. Number Theory 27 (1987), 324-352.
MathSciNet
CrossRef
- C. L. Stewart,
On the representation of an integer in
two different bases,
J. Reine Angew. Math. 319 (1980), 63-72.
MathSciNet
Glasnik Matematicki Home Page
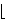 x
x![]](symbol/rceil.gif) be the closest integer to
x. In
this paper, we look at the arithmetic properties of the integers
be the closest integer to
x. In
this paper, we look at the arithmetic properties of the integers
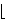 θn
θn![]](symbol/rceil.gif)
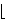 x
x![]](symbol/rceil.gif) be the closest integer to
x. In
this paper, we look at the arithmetic properties of the integers
be the closest integer to
x. In
this paper, we look at the arithmetic properties of the integers
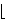 θn
θn![]](symbol/rceil.gif)