Glasnik Matematicki, Vol. 44, No.2 (2009), 267-284.
ON CONVERGENTS FORMED FROM DIOPHANTINE EQUATIONS
Carsten Elsner, Takao Komatsu and Iekata Shiokawa
FHDW, Fachhochschule für die Wirtschaft, University of Applied Sciences,
Freundallee 15, D-30173 Hannover, Germany
e-mail: carsten.elsner@fhdw.de
Graduate School of Science and Technology, Hirosaki University,
Hirosaki, 036-8561 Japan
e-mail: komatsu@cc.hirosaki-u.ac.jp
Department of Mathematics, Keio University, Yokohama, 223-8522 Japan
e-mail: shiokawa@math.keio.ac.jp
Abstract. We compute upper and lower bounds for the approximation of
certain values ξ of hyperbolic and trigonometric functions by rationals x/y
such that x, y satisfy Diophantine equations.
We show that there are infinitely many coprime integers x, y such that
|y ξ - x| 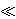 (log log y)/(log y)
(log log y)/(log y)
and a Diophantine equation holds simultaneously relating x, y and some integer z.
Conversely, all positive integers x, y with
y ≥ c0 solving the Diophantine equation satisfy
|y ξ - x|  (log log y)/(log y)
(log log y)/(log y)
Moreover, we approximate sin(πα) and cos(πα)
by rationals in connection with solutions of a quadratic Diophantine
equation when tan(πα/2) is a Liouville number.
2000 Mathematics Subject Classification.
11D09, 11D25, 11J04, 11J70.
Key words and phrases. Diophantine approximation, Diophantine equations,
trigonometric and hyperbolic functions.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.2.02
References:
- E. B. Burger and A. M. Pillai,
On Diophantine approximation along algebraic curves,
Proc. Amer. Math. Soc. 136 (2008), 11-19.
MathSciNet
CrossRef
- H. Cohen,
Number Theory, vol.I: Tools and Diophantine Equations,
Springer, 2007.
MathSciNet
- H. Cohen,
Number Theory, vol.II: Analytic and Modern Tools, Springer, 2007.
MathSciNet
- L. E. Dickson,
History of the theory of numbers,
vol.2, Dover Publications, 2005.
- C. Elsner,
On arithmetic properties of the convergents of Euler's number,
Colloq. Math. 79 (1999), 133-145.
MathSciNet
- C. Elsner,
On rational approximations by Pythagorean numbers,
Fibonacci Quart. 41 (2003), 98-104.
MathSciNet
- C. Elsner, T. Komatsu, and I. Shiokawa,
Approximation of values of hypergeometric functions by restricted rationals,
J. Théorie des Nombres de Bordeaux 19 (2007), 387-399.
MathSciNet
- C. Elsner and T. Komatsu,
A recurrence formula for leaping convergents of non-regular continued fractions,
Linear Algebra Appl. 428 (2008), 824-833.
MathSciNet
CrossRef
- C. Georgikopoulos,
Rational integral solutions of the equations x3+4y3 =
z2 and x3+2y3 = z2,
Bull. Soc. Math. Gréce 24 (1948), 13-19.
MathSciNet
- G. H. Hardy and E. M. Wright,
An introduction to the theory of numbers,
fifth edition, Clarendon Press, Oxford, 1979.
MathSciNet
- T. Komatsu,
Arithmetical properties of the leaping convergents of e1/s,
Tokyo J. Math. 27 (2004), 1-12.
MathSciNet
CrossRef
- L. J. Mordell,
Diophantine equations,
Academic Press, London and New York, 1969.
MathSciNet
- O. Perron,
Die Lehre von den Kettenbrüchen,
Chelsea, New York, 1950.
Glasnik Matematicki Home Page
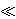 (log log y)/(log y)
(log log y)/(log y)
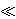 (log log y)/(log y)
(log log y)/(log y)
 (log log y)/(log y)
(log log y)/(log y)