Glasnik Matematicki, Vol. 44, No.1 (2009), 195-210.
DENDRITES AND SYMMETRIC PRODUCTS
Gerardo Acosta, Rodrigo Hernández-Gutiérrez and
Verónica Martinez-de-la-Vega
Instituto de Matemáticas, Universidad Nacional
Autónoma de México, Ciudad Universitaria, México D.F., 04510, México
e-mail: gacosta@matem.unam.mx
e-mail: rod@matem.unam.mx
e-mail: vmvm@matem.unam.mx
Abstract. For a given continuum X and a natural number n, we consider the
hyperspace Fn(X) of all nonempty subsets of X
with at most n points,
metrized by the Hausdorff metric. In this paper we show that if
X is a dendrite whose set of end points is closed,
n 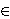 N and
Y is a continuum such that the hyperspaces Fn(X)
and Fn(Y) are
homeomorphic, then Y is a dendrite whose set of end points is closed.
N and
Y is a continuum such that the hyperspaces Fn(X)
and Fn(Y) are
homeomorphic, then Y is a dendrite whose set of end points is closed.
2000 Mathematics Subject Classification.
54B20, 54C15, 54F15, 54F50.
Key words and phrases. Continuum, contractibility, dendrite, finite graph, unique hyperspace.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.1.12
References:
- G. Acosta,
Continua with unique
hyperspace, Lecture Notes in Pure and Applied Mathematics 230,
Marcel Dekker, Inc., New York, 2002, 33-49.
MathSciNet
- G. Acosta and D. Herrera-Carrasco,
Dendrites without unique hyperspace,
Houston J. Math. 35 (2009), 469-484.
- D. Arévalo, W. J. Charatonik, P. Pellicer-Covarruvias and L. Simón,
Dendrites with a closed set of end points, Topology
Appl. 115 (2001), 1-17.
MathSciNet
CrossRef
- R. H. Bing,
Partitioning a set, Bull. Amer. Math. Soc. 55 (1949),
1101-1110.
MathSciNet
CrossRef
- K. Borsuk,
Theory of Retracts, Monografie Matematyczne 44,
Polish Scientific Publishers, Warszawa, Poland, 1967.
MathSciNet
- K. Borsuk and S. Ulam,
On symmetric products of topological
spaces, Bull. Amer. Math. Soc. 37 (1931), 875-882.
MathSciNet
CrossRef
- E. Castaneda and A. Illanes,
Finite graphs have unique symmetric
products, Topology Appl. 153 (2006), 1434-1450.
MathSciNet
CrossRef
- J. J. Charatonik and W. J. Charatonik,
Dendrites, Aportaciones Mat. Comun. 22, Soc. Mat. Mexicana, México (1998),
227--253.
MathSciNet
- J. J. Charatonik and A. Illanes,
Local connectedness in hyperspaces, Rocky Mountain J. Math. 36 (2006), 811-856.
MathSciNet
CrossRef
- D. Curtis and N. T. Nhu,
Hyperspaces of finite subsets which are
homeomorphic to
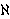 0-dimensional linear metric spaces, Topology
Appl. 19 (1985), 251-260.
0-dimensional linear metric spaces, Topology
Appl. 19 (1985), 251-260.
MathSciNet
CrossRef
- D. Herrera-Carrasco,
Dendrites with unique hyperspace,
Houston J. Math. 33 (2007), 795-805.
MathSciNet
- D. Herrera-Carrasco and F. Macias-Romero,
Dendrites with unique n-fold hyperspace,
Topology Proc. 32 (2008), 321-337.
- D. Herrera-Carrasco, M. de J. López and F. Macias-Romero,
Dendrites with unique symmetric products, to appear in Topology Proc.
- W. Hurewicz and H. Wallman,
Dimension Theory, Princeton University Press, Princeton,
1941.
MathSciNet
- A. Illanes,
Dendrites with unique hyperspace F2(X), JP J. Geom. Topol.
2 (2002), 75-96.
MathSciNet
- A. Illanes,
Dendrites with unique hyperspace C2(X), II,
Topology Proc. 34 (2009), 77-96.
- A. Illanes and S. B. Nadler Jr.,
Hyperspaces. Fundamentals and recent advances, Pure and Applied
Mathematics 216, Marcel Dekker, Inc., New York, 1999.
MathSciNet
- K. Kuratowski,
Topology, Vol. 2, Academic Press and PWN, New
York, London and Warszawa, 1968.
MathSciNet
- J. M. Martinez-Montejano,
Non-confluence of the natural map
of products onto symmetric products, Lecture Notes in Pure and Applied
Mathematics 230, Marcel Dekker, Inc., New York, 2002, 229-236.
MathSciNet
- E. E. Moise,
Grille decomposition and convexification theorems
for compact locally connected continua, Bull. Amer. Math. Soc. 55 (1949),
1111-1121.
MathSciNet
CrossRef
- S. B. Nadler, Jr.,
Continuum theory. An introduction,
Monographs and Textbooks in Pure and Applied Math. 158, Marcel Dekker, Inc., New York, 1992.
MathSciNet
- S. B. Nadler, Jr.,
Dimension theory: an introduction with
exercises, Aportaciones Matemáticas: Textos [Mathematical
Contributions: Texts], 18. Sociedad Matemática Mexicana,
México, 2002.
MathSciNet
- G. T. Whyburn,
Analytic topology, American Mathematical Society Colloquium Publications 28,
American Mathematical Society, New York, 1942, reprinted with corrections 1971.
MathSciNet
- W. Wu,
Note sur les produits essentiels symétriques des espaces
topologiques, C. R. Acad. Sci. Paris 224 (1947), 1139-1141.
MathSciNet
Glasnik Matematicki Home Page
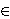 N and
Y is a continuum such that the hyperspaces Fn(X)
and Fn(Y) are
homeomorphic, then Y is a dendrite whose set of end points is closed.
N and
Y is a continuum such that the hyperspaces Fn(X)
and Fn(Y) are
homeomorphic, then Y is a dendrite whose set of end points is closed.
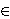 N and
Y is a continuum such that the hyperspaces Fn(X)
and Fn(Y) are
homeomorphic, then Y is a dendrite whose set of end points is closed.
N and
Y is a continuum such that the hyperspaces Fn(X)
and Fn(Y) are
homeomorphic, then Y is a dendrite whose set of end points is closed.
 0-dimensional linear metric spaces, Topology
Appl. 19 (1985), 251-260.
0-dimensional linear metric spaces, Topology
Appl. 19 (1985), 251-260.