Glasnik Matematicki, Vol. 44, No.1 (2009), 11-81.
ON THE RESIDUAL SPECTRUM OF HERMITIAN
QUATERNIONIC INNER FORM OF SO8
Neven Grbac
Department of Mathematics, University of Rijeka, Omladinska 14, 51000 Rijeka, Croatia
e-mail: neven.grbac@math.uniri.hr
Abstract. In this paper we decompose the residual spectrum supported in the
minimal parabolic subgroup of an inner form of the split group
SO8. The approach is the Langlands spectral theory. However,
since the group is non-quasi-split, it is out of the scope of
the Langlands-Shahidi method and the new technique for the
normalization of standard intertwining operators is developed. The
decomposition shows interesting parts of the residual spectrum not
appearing in the case of quasi-split groups.
2000 Mathematics Subject Classification.
11F70, 22E55.
Key words and phrases. Automorphic forms, spectral decomposition, residual
spectrum, inner forms.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.1.03
References:
- J. Arthur,
Intertwining Operators and Residues I. Weighted
Characters, J. Funct. Anal. 84 (1989), 19-84.
MathSciNet
CrossRef
- J. Arthur,
Unipotent automorphic representations:
conjectures, in: Orbites unipotentes et représentations
II, Astérisque 171-172 (1989), 13-71.
MathSciNet
- J. Arthur,
Unipotent automorphic representations: global
motivation, in: L. Clozel, J. S. Milne, eds., Automorphic
Forms, Shimura Varieties, and L--functions I., Academic
Press, 1990, 1-75.
MathSciNet
- J. Arthur,
An Introduction to the trace formula, in:
Harmonic analysis, the trace formula and Shimura varieties, 2005, 1-263.
MathSciNet
- J. Arthur and L. Clozel,
Simple algebras, base change, and
the advanced theory of the trace formula, Princeton Univiversity Press, Princeton, 1989.
MathSciNet
- I. N. Bernstein and A. V. Zelevinsky,
Induced representations of
reductive
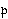 -adic Groups I,
Ann. Sci. École
Norm. Sup. (4) 10 (1977), 441-472.
-adic Groups I,
Ann. Sci. École
Norm. Sup. (4) 10 (1977), 441-472.
MathSciNet
Numdam
- W. Casselman and F. Shahidi,
On irreducibility of standard
modules for generic representations, Ann. Sci. École Norm.
Sup. (4) 31 (1998), 561-589.
MathSciNet
CrossRef
- P. Deligne, D. Kazhdan and M. F. Vignéras,
Représentations
des algèbres centrales simples p-adiques, Représentations des Groupes
Réductifs sur un Corps Local,
Herman, Paris, 1984, 33-117.
MathSciNet
- S. Gelbart and H. Jacquet,
A relation between automorphic
representations of GL(2) and GL(3), Ann. Sci. Éc.
Norm. Sup. (4) 11 (1978), 471-542.
MathSciNet
Numdam
- S. Gelbart and H. Jacquet,
Forms of GL(2) from the analytic
point of view, in: Automorphic forms, representations and L-functions,
Proc. Sympos. Pure Math. 33, part 1, 1979, 213-251.
MathSciNet
- N. Grbac,
Correspondence between the residual spectra of
rank two split classical groups and their inner forms, in:
Functional analysis IX (Dubrovnik, 2005), 44-57, Various Publ.
Ser. 48, Univ. Aarhus, Aarhus, 2007.
MathSciNet
- N. Grbac,
On a relation between residual spectra of split
classical groups and their inner forms, Canad. J. Math., to
appear.
- N. Grbac,
The residual spectrum of an inner form of Sp8
supported in the minimal parabolic subgroup, Trans. Amer.
Math. Soc., to appear.
- N. Grbac,
The residual spectrum of GLn over a division
algebra, an appendix to: A. I. Badulescu, Global
Jacquet-Langlands correspondence, multiplicity one and
classification of automorphic representations, Invent.
Math. 172 (2008), 383-438.
MathSciNet
- N. Grbac,
Arthur parameters for the residual spectrum of
certain low rank Hermitian quaternionic classical groups, in
preparation.
- M. Hanzer,
R groups for quaternionic Hermitian groups,
Glas. Mat. Ser. III 39(59) (2004), 31-48.
MathSciNet
CrossRef
- M. Hanzer,
The unitary dual of the Hermitian quaternionic
group of split rank 2, Pacific J. Math. 226 (2006),
353-388.
MathSciNet
- H. Jacquet,
Principal L-functions of the linear group, Proc. Sympos. Pure Math.
33, part 2, 1979, 63-86.
MathSciNet
- H. Jacquet,
On the residual spectrum of GL(N), Lie
Group Representations II, Lecture Notes in Math. 1041,
Springer, Berlin, 1984, 185-208.
MathSciNet
- H. Jacquet, I. I. Piatetskii-Shapiro and J. A. Shalika,
Rankin-Selberg convolutions, Amer. J. Math. 105
(1983), 367-464.
MathSciNet
CrossRef
- C. D. Keys and F. Shahidi,
Artin L-functions and normalization
of intertwining operators, Ann. Sci. École Norm. Sup. (4)
21 (1988), 67-89.
MathSciNet
Numdam
- H. H. Kim,
The residual spectrum of Sp4, Compositio
Math. 99 (1995), 129-151.
MathSciNet
Numdam
- H. H. Kim,
The residual spectrum of G2, Canad. J.
Math. 48 (1996), 1245-1272.
MathSciNet
- H. H. Kim, Langlands-Shahidi method and poles of automorphic
L-functions: application to exterior square L-functions,
Canad. J. Math. 51 (1999), 835-849.
MathSciNet
- H. H. Kim,
Langlands-Shahidi method and poles of automorphic
L-functions II, Israel J. Math. 117 (2000), 261-284.
MathSciNet
CrossRef
- H. H. Kim,
Residual spectrum of odd orthogonal groups,
Internat. Math. Res. Notices 17 (2001), 873-906.
MathSciNet
CrossRef
- T. Kon-No,
The residual spectrum of U(2,2), Trans.
Amer. Math. Soc. 350 (1998), 1285-1358.
MathSciNet
CrossRef
- B. Kostant,
On Whittaker vectors and representation theory,
Invent. Math. 48 (1978), 101-184.
MathSciNet
CrossRef
- J.-P. Labesse, R. P. Langlands,
L-indistinguishability for
SL(2), Canad. J. Math. 31 (1979), 726-785.
MathSciNet
- R. P. Langlands,
On the functional equations satisfied
by Eisenstein series, Lecture Notes in Math. 544,
Springer-Verlag, 1976.
MathSciNet
- R. P. Langlands,
On the notion of an automorphic
representation, A supplement to the paper: A. Borel and H. Jacquet,
Automorphic forms and automorphic representations, Proc.
Sympos. Pure Math. 33, part 1 (1979), 203-207.
MathSciNet
- E. Lapid, G. Muic and M. Tadic,
On the generic unitary
dual of quasisplit classical groups, Int. Math. Res.
Not. 26 (2004), 1335-1354.
MathSciNet
CrossRef
- C. Moeglin,
Orbites unipotentes et spectre discret non
ramifie, Compositio Math. 77 (1991), 1-54.
MathSciNet
Numadam
- C. Moeglin,
Représentations unipotentes et formes
automorphes de carré intégrable, Forum Math. 6
(1994), 651-744.
MathSciNet
- C. Moeglin,
Conjectures sur le spectre residuel, J.
Math. Soc. Japan 53 (2001), 395-427.
MathSciNet
CrossRef
- C. Moeglin,
Formes automorphes de carré intégrable
non cuspidales, preprint.
- C. Moeglin and J.-L. Waldspurger,
Le spectre résiduel de
GL(n), Ann. Sci. École Norm. Sup. (4) 22 (1989),
605-674.
MathSciNet
Numdam
- C. Moeglin and J.-L. Waldspurger,
Spectral decomposition and Eisenstein series: Une paraphrase de l'Ecriture,
Cambridge Tracts in Math. 113, Cambridge University Press, Cambridge, 1995.
MathSciNet
- G. Muic,
Some results on square integrable
representations; irreducibility of standard representations,
Internat. Math. Res. Notices 14 (1998), 705-726.
MathSciNet
CrossRef
- G. Muic,
A proof of Casselman-Shahidi's conjecture for
quasi-split classical groups, Canad. Math. Bull. 44
(2001), 298-312.
MathSciNet
CrossRef
- G. Muic,
On certain classes of unitary representations
for split classical groups, Canad. J. Math. 59 (2007),
148-185.
MathSciNet
- G. Muic and G. Savin,
Complementary series for Hermitian
quaternionic groups, Canad. Math. Bull. 43 (2000),
90-99.
MathSciNet
- F. Shahidi,
On certain L-functions, Amer. J. Math.
103 (1981), 297-355.
MathSciNet
CrossRef
- F. Shahidi,
Local coefficients as Artin factors for real
groups, Duke Math. J. 52 (1985), 973-1007.
MathSciNet
CrossRef
- F. Shahidi,
A proof of Langlands' conjecture on Plancherel
measures; complementary series of
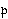 -adic groups,
Ann. of Math. 132 (1990), 273-330.
-adic groups,
Ann. of Math. 132 (1990), 273-330.
MathSciNet
CrossRef
- F. Shahidi,
Twisted endoscopy and reducibility of induced
representations for p-adic groups, Duke Math. J. 66 (1992), 1-41.
MathSciNet
CrossRef
- B. Speh,
The unitary dual of Gl(3,R) and
Gl(4,R), Math. Ann. 258 (1981/1982), 113-133.
MathSciNet
CrossRef
- M. Tadic,
Induced representations of GL(n,A) for
p-adic division algebras A, J. Reine Angew. Math. 405 (1990), 48-77.
MathSciNet
- M. Tadic,
Notes on representations of non--archimedean
SL(n), Pacific J. Math. 152 (1992), 375-396.
MathSciNet
- D. Vogan,
Gelfand-Kirillov dimension for Harish-Chandra
modules, Invent. Math. 48 (1978), 75-98.
MathSciNet
CrossRef
- N. R. Wallach,
Real reductive groups I, Pure and
Applied Math. 132, Academic Press, Inc., Boston, 1988.
MathSciNet
- G. Warner,
Harmonic analysis on semi--simple Lie groups I,
Die Grundlehren der mathematischen Wissenschaften 188,
Springer-Verlag, New York-Heidelberg, 1972.
MathSciNet
- A. V. Zelevinsky,
Induced representations of reductive
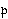 -adic groups II. On irreducible representations of
GL(n), Ann. Sci. École Norm. Sup. (4) 13 (1980),
165-210.
-adic groups II. On irreducible representations of
GL(n), Ann. Sci. École Norm. Sup. (4) 13 (1980),
165-210.
MathSciNet
Numdam
- Y. Zhang,
The holomorphy and nonvanishing of normalized
local intertwining operators, Pacific J. Math. 180
(1997), 385-398.
MathSciNet
- S. Zampera,
The residual spectrum of the group of type
G2, J. Math. Pures Appl. 76 (1997), 805-835.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
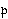 -adic Groups I,
Ann. Sci. École
Norm. Sup. (4) 10 (1977), 441-472.
-adic Groups I,
Ann. Sci. École
Norm. Sup. (4) 10 (1977), 441-472. 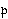 -adic groups,
Ann. of Math. 132 (1990), 273-330.
-adic groups,
Ann. of Math. 132 (1990), 273-330. 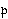 -adic groups II. On irreducible representations of
GL(n), Ann. Sci. École Norm. Sup. (4) 13 (1980),
165-210.
-adic groups II. On irreducible representations of
GL(n), Ann. Sci. École Norm. Sup. (4) 13 (1980),
165-210.