Glasnik Matematicki, Vol. 43, No.2 (2008), 321-335.
FINITE NONNILPOTENT GROUPS WITH FEW HEIGHTS OF NONNORMAL SUBGROUPS
Yakov Berkovich
Department of Mathematics, University of Haifa, Mount Carmel, Haifa 31905, Israel
e-mail: berkov@math.haifa.ac.il
Abstract. The number of prime factors of the order of a group G
(multiplicities counted) is said to be the height of G and
denoted by nλ(G). We classify the nonnilpotent groups G
with nλ(G) = 2
and nonsolvable groups G with
nλ(G) 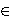 {3,4}.
{3,4}.
2000 Mathematics Subject Classification.
20D25.
Key words and phrases. Height, solvable group, Carter subgroup.
Full text (PDF) (free access)
DOI: 10.3336/gm.43.2.07
References:
- Y. Berkovich,
Nonnormal and minimal nonabelian subgroups of a
finite group, submitted.
- Y. Berkovich,
Some criteria for the solvability of finite groups, Sibirsk. Mat. Z. 4 (1963), 723-728.
MathSciNet
- Ya. G. Berkovich and E. M. Zhmud,
Characters of Finite Groups. Part 1, Translations of Mathematical Monographs 172, American
Mathematical Society, Providence, RI, 1998.
MathSciNet
- N. Blackburn,
Generalizations of certain elementary theorems
on p-groups, Proc. London Math. Soc. (3) 11 (1961), 1-22.
MathSciNet
CrossRef
- L. E. Dickson,
Linear groups with an exposition of the Galois
field theory, Dover Publications, Inc., New York, 1958.
MathSciNet
- B. Huppert,
Endliche Gruppen. I, Springer-Verlag, Berlin-New York, 1967.
MathSciNet
- Yu. A. Gol'fand,
On groups all of whose subgroups are special,
Doklady Akad. Nauk SSSR 60 (1948), 1313-1315.
MathSciNet
- D. S. Passman,
Nonnormal subgroups of p-groups,
J. Algebra 15 (1970), 352-370.
MathSciNet
CrossRef
- L. Redei,
Die endlichen einstufig nichtnilpotenten Gruppen,
Publ. Math. Debrecen 4 (1956), 303-324.
MathSciNet
- O. Schmidt,
Groups all of whose subgroups are nilpotent,
Mat. Sb. 31 (1924), 366-372.
Jahrbuch
- O. Schmidt,
Groups having only one class of nonnormal subgroups,
Mat. Sb. 33 (1926), 161-172.
Jahrbuch
- O. Schmidt,
Groups with two classes of nonnormal subgroups,
Proc. Seminar on group theory (1938), 7-26.
- I. Schur,
Über die Darstellung der endlichen Gruppen durch
gebrochene lineare Substitutionen,
J. Reine Angew. Math. 127 (1904), 20-50.
Jahrbuch
- J. G. Thompson,
Nonsolvable finite groups all of whose local
subgroups are solvable, Bull. Amer. Math. Soc. 74 (1968), 383-437.
MathSciNet
CrossRef
- J. H. Walter,
The characterization of finite groups with abelian
Sylow 2-subgroup, Ann. Math. (2) 89 (1969), 405-514.
MathSciNet
CrossRef
- G. Zappa,
Finite groups in which all nonnormal subgroups have
the same order, Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat.
Natur. Rend. Lincei (9) Mat. Appl. 13 (2002), 5-16; II,
ibid 14 (2003), 13-21.
MathSciNet
MathSciNet
Glasnik Matematicki Home Page
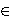 {3,4}.
{3,4}.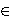 {3,4}.
{3,4}.