Glasnik Matematicki, Vol. 43, No.2 (2008), 265-291.
ON THE EXTENSIBILITY OF DIOPHANTINE TRIPLES {k-1, k+1, 4k}
FOR GAUSSIAN INTEGERS
Zrinka Franušić
Department of Mathematics, University of Zagreb, 10 000 Zagreb, Croatia
e-mail: fran@math.hr
Abstract. In this paper, we prove that if
{k-1, k+1, 4k, d}, where
k 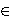 Z[i] \ {0, ± 1},
d
Z[i] \ {0, ± 1},
d 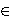 Z[i], is a Diophantine quadruple in
Z[i], i.e. if (k-1)d+1,
(k+1)d+1, 4kd+1 are perfect
squares in Z[i], then d = 16k3-4k.
Z[i], is a Diophantine quadruple in
Z[i], i.e. if (k-1)d+1,
(k+1)d+1, 4kd+1 are perfect
squares in Z[i], then d = 16k3-4k.
2000 Mathematics Subject Classification.
11D09, 11R11.
Key words and phrases. Diophantine quadruples, simultaneous Diophantine equations,
linear recurrence sequences.
Full text (PDF) (free access)
DOI: 10.3336/gm.43.2.04
References:
- J. Arkin, V. E. Hoggatt and E. G. Strauss,
On Euler's solution of a problem of Diophantus,
Fibonacci Quart. 17 (1979), 333-339.
MathSciNet
- A. Baker and H. Davenport,
The equations 3x2 - 2 = y2 and
8x2 - 7 = z2, Quart. J.
Math. Oxford Ser. (2) 20 (1969), 129-137.
MathSciNet
CrossRef
- A. Baker and G. Wüstholz,
Logarithmic forms and group varieties,
J. Reine Angew. Math. 442 (1993), 19-62.
MathSciNet
- M. A. Bennett,
On the number of solutions of simultaneous Pell equations,
J. Reine Angew. Math. 498 (1998), 173-199.
MathSciNet
CrossRef
- Y. Bugeaud, A. Dujella and M. Mignotte,
On the family of Diophantine triples
{k-1, k+1, 16k3-4k},
Glasgow Math. J. 49 (2007), 333-344.
MathSciNet
CrossRef
- A. Dujella,
The problem of extension of parametric family of Diophantine
triples, Publ. Math. Debrecen 51 (1997), 311-322.
MathSciNet
- A. Dujella,
A proof of the Hoggatt-Bergum conjecture,
Proc. Amer. Math. Soc. 127 (1999), 1999-2005.
MathSciNet
CrossRef
- A. Dujella,
An absolute bound for the size of Diophantine m-tuples,
J. Number Theory 89 (2001), 126-150.
MathSciNet
CrossRef
- A. Dujella,
There are only finitely many Diophantine quintuples,
J. Reine Angew. Math. 566 (2004), 183-214.
MathSciNet
CrossRef
- A. Dujella and A. Pethö,
Generalization of a theorem of Baker and Davenport,
Quart. J. Math. Oxford Ser. (2) 49 (1998), 291-306.
MathSciNet
CrossRef
- L. Fjellstedt,
On a class of Diophantine equations of the second degree in imaginary quadratic fields,
Ark. Mat. 2 (1953), 435-461.
MathSciNet
CrossRef
- Y. Fujita,
The extensibility of Diophantine pairs {k-1, k+1},
J. Number Theory 128 (2008), 322-353.
MathSciNet
CrossRef
- P. Gibbs,
Some rational Diophantine sextuples,
Glas. Mat. Ser. III 41(61) (2006), 195-203.
MathSciNet
CrossRef
- B. Jadrijevic and V. Ziegler,
A system of relative Pellian equations and related family of
relative Thue equations, Int. J. Number Theory 2 (2006), 569-590.
MathSciNet
CrossRef
- I. Niven, H. S. Zuckerman and H. L. Montgomery,
An Introduction to the Theory of Numbers, Wiley, New York, 1991.
MathSciNet
- W. Sierpinski,
Elementary Theory of Numbers, PWN,
Warszawa; North Holland, Amsterdam, 1988.
MathSciNet
Glasnik Matematicki Home Page
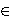 Z[i] \ {0, ± 1},
Z[i] \ {0, ± 1},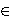 Z[i],
Z[i],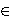 Z[i] \ {0, ± 1},
Z[i] \ {0, ± 1},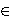 Z[i],
Z[i],