Glasnik Matematicki, Vol. 43, No.1 (2008), 205-217.
ONE MORE VARIATION OF THE POINT-OPEN GAME
Arcos Daniel Jardón and Vladimir V. Tkachuk
Departamento de Matemáticas, Universidad Autónoma Metropolitana,
San Rafael Atlixco, 186, Col. Vicentina, Iztapalapa, C.P. 09340, México
e-mail: jardon60@hotmail.com
e-mail: vova@xanum.uam.mx
Abstract. A topological game "Dense
Gδσ-sets" (also denoted by
DG)
is introduced as follows: for any
n 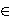 ω at the n-th
move the player I takes a point
xn v X and
II responds by taking a Gδ-set Qn in the
space X such that xn
ω at the n-th
move the player I takes a point
xn v X and
II responds by taking a Gδ-set Qn in the
space X such that xn 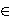 Qn. The play stops after
ω moves and I wins if the set
Qn. The play stops after
ω moves and I wins if the set
 {Qn :
n
{Qn :
n 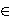 ω}
is dense in X. Otherwise the player II is declared to be the winner.
We study classes of spaces on
which the player I has a winning strategy. It is evident
that the I-favorable spaces constitute a generalization of
the class of separable spaces. We show that there exists a
neutral space for the game
DG
and prove, among
other things, that Lindelöf scattered spaces and dyadic spaces
are I-favorable. We characterize I-favorability for the game
DG
in the spaces
Cp(X); one of the applications is that, for a Lindelöf
Σ-space X, the space Cp(X) is I-favorable for
DG
if and only if X is
ω-monolithic.
ω}
is dense in X. Otherwise the player II is declared to be the winner.
We study classes of spaces on
which the player I has a winning strategy. It is evident
that the I-favorable spaces constitute a generalization of
the class of separable spaces. We show that there exists a
neutral space for the game
DG
and prove, among
other things, that Lindelöf scattered spaces and dyadic spaces
are I-favorable. We characterize I-favorability for the game
DG
in the spaces
Cp(X); one of the applications is that, for a Lindelöf
Σ-space X, the space Cp(X) is I-favorable for
DG
if and only if X is
ω-monolithic.
2000 Mathematics Subject Classification.
54H11, 54C10, 22A05, 54D25, 54C25.
Key words and phrases. Topological game, player, winning strategy,
dense Gδσ-sets, separable space, dyadic
compact space, scattered compact space, neutral space, function
space.
Full text (PDF) (free access)
DOI: 10.3336/gm.43.1.14
References:
- A. V. Arhangel'skii,
The structure
and classification of topological spaces and cardinal invariants,
Uspehi Mat. Nauk 33 (1978), 29-84 (in Russian).
MathSciNet
- A. V. Arhangel'skii,
Topological Function Spaces, Kluwer Acad. Publ., Dordrecht, 1992.
MathSciNet
- S. Baldwin,
Possible point-open types of subsets of the reals, Topology Appl. 38 (1991),
219--23.
MathSciNet
CrossRef
- P. Daniels and G. Gruenhage,
The point-open types of subsets of the reals,
Topology Appl. 37 (1990), 53-64.
MathSciNet
CrossRef
- R. Engelking,
General Topology, Heldermann Verlag, 1989.
MathSciNet
- F. Galvin,
Indeterminacy of point-open games, Bull. Acad. Polon. Sci., Sér. Math.
26 (1978), 445-449.
MathSciNet
- R. Hodel,
Cardinal functions I,
Handbook of Set-Theoretic Topology, ed. by K. Kunen and
J. E. Vaughan, Elsevier Sci. Publ., B.V., 1984, 1-61.
MathSciNet
- R. Telgársky,
Spaces defined by topological games,
Fund. Math. 88 (1975), 193-223.
MathSciNet
- R. Telgársky,
Spaces defined by topological games, II, Fund. Math. 116 (1983),
189-207.
MathSciNet
- V. V. Tkachuk,
Topological applications of game theory, Moscow State
University P.H., Moscow, 1992 (in Russian).
- V. V. Tkachuk,
Some new versions of an old game, Comment. Math. Univ. Carolinae 36 (1995),
177-196.
MathSciNet
Glasnik Matematicki Home Page
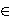 ω
ω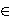 Qn
Qn {Qn :
n
{Qn :
n 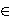 ω}
ω}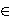 ω
ω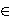 Qn
Qn {Qn :
n
{Qn :
n 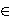 ω}
ω}