Glasnik Matematicki, Vol. 42, No.2 (2007), 309-318.
ORTHOGONALITY, SATURATION AND SHAPE
Luciano Stramaccia
Dipartimento di Matematica e Informatica, Università di Perugia,
via Pascoli, 06123 Perugia, Italia
e-mail: stra@dipmat.unipg.it
Abstract. The class of shape equivalences for a
pair (C,
K)
of categories is the orthogonal of
K, that is
Σ =
K
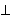 .
Then Σ is internally saturated
(Σ = Σ
.
Then Σ is internally saturated
(Σ = Σ
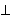 ).
On the other hand, every internally saturated class of morphisms
Σ
).
On the other hand, every internally saturated class of morphisms
Σ 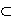 Mor(C),
is the class of shape
equivalences for some pair
(C,
K).
Moreover, every
class of shape equivalences Σ enjoys a calculus of left
fractions and such a fact allows one to use techniques from
categories of fractions to
obtain conditions for
Σ
Mor(C),
is the class of shape
equivalences for some pair
(C,
K).
Moreover, every
class of shape equivalences Σ enjoys a calculus of left
fractions and such a fact allows one to use techniques from
categories of fractions to
obtain conditions for
Σ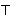 to be
reflective or proreflective in C.
to be
reflective or proreflective in C.
2000 Mathematics Subject Classification.
18A40, 18A25, 54B30, 55P55.
Key words and phrases. Orthogonality, internal saturation, calculus of
fractions, shape, shape equivalences.
Full text (PDF) (free access)
DOI: 10.3336/gm.42.2.06
References:
- C. Casacuberta and A. Frei,
On saturated classes of morphisms,
Theory Appl. Categ. 7 (2000) 43-46.
MathSciNet
- C. Casacuberta and A. Frei, Localizations and
idempotent approximations to complections,
J. Pure Appl. Algebra 142 (1999), 25-33.
MathSciNet
CrossRef
- C. Cassidy, A. Hebert and G.M. Kelly, Reflective
subcategories, localizations and factorization Systems,
J. Austral. Math. Soc. 38 (1985), 287-329.
MathSciNet
- J. M. Cordier and T. Porter, Categorical Shape Theory,
World Scientific, 1986.
- A. Grothendieck and J. L. Verdier, Prefaisceaux,
SGA 4, LN. 269,
Springer Verlag, Berlin-Heidelberg-New York, 1969.
- P. Gabriel and M. Zisman, Calculus of Fractions and
Homotopy Theory, Springer Verlag, Berlin-Heidelberg-New York, 1968.
MathSciNet
- S. Mardesic and J. Segal, Shape Theory, North
Holland, 1982.
MathSciNet
- S. Mardesic, Strong Shape and Homology,
Springer Monographs in Mathematics, Springer Verlag, Berlin-Heidelberg-New York, 2000.
MathSciNet
- L. Popescu and N. Popescu, Theory of Categories,
Sijthoff-Noordhoff Int. Publ., 1979.
- H. Schubert, Categories, Springer Verlag, 1974.
MathSciNet
- L. Stramaccia, Groupoids and strong shape,
Topology Appl. 153 (2005), 528-539.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
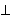 .
.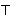
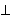 ).
).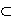 Mor(C),
Mor(C),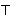
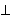 .
.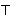
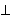 ).
).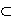 Mor(C),
Mor(C),