Glasnik Matematicki, Vol. 42, No.1 (2007), 195-211.
THE Sn-EQUIVALENCE OF COMPACTA
Nikica Uglešić and Branko Červar
University of Zadar, Studentski dom, F. Tuđmana 24 D, 23000 Zadar,
Croatia
e-mail: nuglesic@unizd.hr
Department of Mathematics, University of Split, Teslina ulica 12/III,
21000 Split, Croatia
e-mail: brankoch@pmfst.hr
Abstract. By reducing the Mardešić S-equivalence to a
finite case, i.e., to each
n 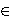 {0}
{0} 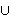 N
separately, we have derived the notions of
Sn-equivalence
and Sn+1-domination of compacta.
The Sn-equivalence for all n
coincides with the S-equivalence. Further, the
Sn+1-equivalence implies
Sn+1-domination, and the
Sn+1-domination implies
Sn-equivalence. The
S0-equivalence is a trivial equivalence relation, i.e., all non
empty compacta are mutually S0-equivalent. It is proved that
the S1-equivalence is strictly finer than the
S0-equivalence, and that the
S2-equivalence is strictly
finer than the S1-equivalence.
Thus, the S-equivalence is
strictly finer than the S1-equivalence. Further, the
S1-equivalence classifies compacta which are
homotopy (shape) equivalent to ANR's up to the homotopy (shape) types. The
S2-equivalence class of an FANR coincides with its
S-equivalence class as well as with its shape type class.
Finally, it is conjectured that, for every n, there exists
n' > n such that the
Sn'-equivalence is strictly
finer than the Sn-equivalence.
N
separately, we have derived the notions of
Sn-equivalence
and Sn+1-domination of compacta.
The Sn-equivalence for all n
coincides with the S-equivalence. Further, the
Sn+1-equivalence implies
Sn+1-domination, and the
Sn+1-domination implies
Sn-equivalence. The
S0-equivalence is a trivial equivalence relation, i.e., all non
empty compacta are mutually S0-equivalent. It is proved that
the S1-equivalence is strictly finer than the
S0-equivalence, and that the
S2-equivalence is strictly
finer than the S1-equivalence.
Thus, the S-equivalence is
strictly finer than the S1-equivalence. Further, the
S1-equivalence classifies compacta which are
homotopy (shape) equivalent to ANR's up to the homotopy (shape) types. The
S2-equivalence class of an FANR coincides with its
S-equivalence class as well as with its shape type class.
Finally, it is conjectured that, for every n, there exists
n' > n such that the
Sn'-equivalence is strictly
finer than the Sn-equivalence.
2000 Mathematics Subject Classification.
55P55.
Key words and phrases. Compactum, ANR, shape, S-equivalence.
Full text (PDF) (free access)
DOI: 10.3336/gm.42.1.14
References:
- K. Borsuk,
Some quantitative properties of shapes,
Fund. Math. 93 (1976), 197-212.
MathSciNet
- D. A. Edwards and R. Geoghegan,
Shapes of complexes,
ends of manifolds, homotopy limits and the Wall obstruction,
Ann. of Math. (2) 101 (1975), 521-535, Correction. Ibid.
104 (1976), 389.
MathSciNet
CrossRef
- K. R. Goodearl and T. B. Rushing,
Direct limit groups
and the Keesling-Mardesic shape fibration,
Pacific J. Math. 86 (1980), 471-476.
MathSciNet
- H. M. Hastings and A. Heller,
Splitting homotopy
idempotents, in: Shape theory and geometric topology (Dubrovnik,
1981), Lecture Notes in Math. 870, Springer, Berlin-New
York, 1981, 23-36.
MathSciNet
- J. Keesling and S. Mardesic,
A shape fibration with fibers of different shape, Pacific J. Math.
84 (1979), 319-331.
MathSciNet
- S. Mardesic,
Comparing fibres in a shape
fibration, Glasnik Mat. Ser. III 13(33) (1978),
317-333.
MathSciNet
- S. Mardesic and J. Segal, Shape Theory, North-Holland
Publishing Co., Amsterdam-New York-Oxford 1982.
MathSciNet
- S. Mardesic and N. Uglesic,
A category whose isomorphisms induce an equivalence relation coarser
than shape, Topology Appl. 153 (2005), 448-463.
MathSciNet
CrossRef
- K. Morita,
The Hurewicz and the Whitehead theorems in
shape theory, Sci. Rep. Tokyo Kyoiku Daigaku Sect. A 12
(1974), 246-258.
MathSciNet
- N. Uglesic,
A note on the Borsuk quasi-equivalence, submitted.
- N. Uglesic and B. Cervar,
A subshape spectrum for compacta,
Glasnik Mat. Ser. III 40(60) (2005), 351-388.
MathSciNet
- C. T. C. Wall,
Finiteness conditions for CW-complexes, Ann.
of Math. (2) 81 (1965), 59-69.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
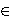 {0}
{0} 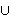 N
N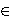 {0}
{0} 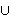 N
N