Glasnik Matematicki, Vol. 42, No.1 (2007), 189-194.
THE STABLE SHAPE OF COMPACT SPACES WITH COUNTABLE COHOMOLOGY GROUPS
Slawomir Nowak
Institute of Mathematics, University of Warsaw,
ul. Banacha 2, 02-097 Warszawa, Poland
e-mail: snowak@mimuw.edu.pl
Abstract. Let X be a compact Hausdorff space and
q 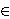 Z
be an integer such that the integral cohomology groups
Hn(X;Z)
are countable for n > q and the stable
cohomotopy groups πsn(X)
of X are countable for n ≥ q.
Then there exists a compact metrizable compact space Y
with the same stable shape as X.
Z
be an integer such that the integral cohomology groups
Hn(X;Z)
are countable for n > q and the stable
cohomotopy groups πsn(X)
of X are countable for n ≥ q.
Then there exists a compact metrizable compact space Y
with the same stable shape as X.
2000 Mathematics Subject Classification.
55P55, 55P40, 55N05, 55Q07.
Key words and phrases. Stable cohomotopy groups, stable shape.
Full text (PDF) (free access)
DOI: 10.3336/gm.42.1.13
References:
- J. F. Adams,
Stable Homotopy and Generalized Homology,
University of Chicago Press, Chicago, 1974.
MathSciNet
- K. Borsuk,
Theory of Shape, PWN-Polish Scientific Publishers,
Warszawa, 1975.
MathSciNet
- D. S. Kahn, J. Kaminker and C. Schochet,
Generalized homology theories on compact metric spaces, Michigan Math. J.
24 (1977), 203--224.
MathSciNet
CrossRef
- S. Mardesic and J. Segal, Shape Theory, North-Holland
Publishing Co., Amsterdam-New York-Oxford 1982.
MathSciNet
- H. R. Margolis,
Spectra and the Steenrod Algebra. Modules over
the Steenrod algebra and the stable homotopy category,
North-Holland Publishing Co., Amsterdam, 1983.
MathSciNet
- T. Miyata,
Generalized stable shape and duality, Topology Appl. 109 (2001), 75-88.
MathSciNet
CrossRef
- T. Miyata and J. Segal,
Generalized stable shape and the Whitehead theorem,
Topology Appl. 63 (1995), 139-164.
MathSciNet
CrossRef
- T. Miyata and J. Segal,
Generalized stable shape and Brown's representation theorem,
Topology Appl. 94 (1999), 275-305.
MathSciNet
CrossRef
- S. Nowak,
On the relationships between shape properties of
subcompacta of Sn and homotopy properties of their
complements, Fund. Math. 128 (1987), 47-60.
MathSciNet
- S. Nowak,
Stable cohomotopy groups of compact spaces, Fund.
Math. 180 (2003), 99-137.
MathSciNet
- R. M. Switzer,
Algebraic Topology - Homotopy and Homology,
Springer-Verlag, New York-Heidelberg, 1975.
MathSciNet
- C. T. C. Wall,
Finiteness conditions for CW-complexes, Ann.
of Math. (2) 81 (1965), 59-69.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
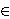 Z
Z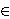 Z
Z