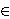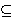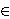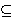Glasnik Matematicki, Vol. 42, No.1 (2007), 95-108.

CLOSED EMBEDDINGS INTO LIPSCOMB'S UNIVERSAL SPACE

Ivan Ivanšić and Uroš Milutinović

FNM, University of Maribor, Koroška cesta 160, 2000 Maribor, Slovenia
e-mail: uros.milutinovic@uni-mb.si

Abstract.   Let J(τ) be Lipscomb's one-dimensional space and L_n(τ) = {x 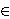J(τ)ⁿ⁺¹ | at least one coordinate of x is irrational} 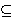J(τ)ⁿ⁺¹ Lipscomb's n-dimensional universal space of weight τ ≥ א_o. In this paper we prove that if X is a complete metrizable space and dim X ≤ n, w X ≤ τ, then there is a closed embedding of X into L_n(τ). Furthermore, any map f : X → J(τ)ⁿ⁺¹ can be approximated arbitrarily close by a closed embedding ψ : X → L_n(τ). Also, relative and pointed versions are obtained. In the separable case an analogous result is obtained, in which the classic triangular Sierpinski curve (homeomorphic to J(3)) is used instead of J(א_o).

2000 Mathematics Subject Classification.   54F45.

Key words and phrases.   Covering dimension, embedding, closed embedding, universal space, generalized Sierpinski curve, Lipscomb's universal space, extension, complete metric space.

DOI: 10.3336/gm.42.1.08

References:

1. R. Engelking, Dimension Theory, PWN-Polish Scientific Publishers, Warszawa and North-Holland Publishing Co., Amsterdam-Oxford-New York, 1978.
   MathSciNet

2. R. Engelking, General Topology, Revised and completed edition, Heldermann Verlag, Berlin, 1989.
   MathSciNet

3. Y. Hattori, A note on universal spaces for finite dimensional complete metric spaces, Glas. Mat. Ser. III 24(44) (1989), 139-147.
   MathSciNet

4. I. Ivansic and U. Milutinovic, A universal separable metric space based on the triangular Sierpinski curve, Topology Appl. 120 (2002), 237-271.
   MathSciNet     CrossRef

5. I. Ivansic and U. Milutinovic, Relative embeddability into Lipscomb's 0-dimensional universal space, Houston J. Math. 29 (2003), 1001-1012.
   MathSciNet

6. I. Ivansic and U. Milutinovic, The pointed version of Lipscomb's embedding theorem, Houston J. Math. 31 (2005), 173-192.
   MathSciNet

7. S. L. Lipscomb, A universal one-dimensional metric space, in: TOPO 72 - General Topology and its Applications (Proc. Second Pittsburgh Internat. Conf., Pittsburgh, 1972.), Lecture Notes in Math. 378, Springer, Berlin, 1974., 248-257.
   MathSciNet

8. S. L. Lipscomb, On imbedding finite-dimensional metric spaces, Trans. Amer. Math. Soc. 211 (1975), 143-160.
   MathSciNet     CrossRef

9. U. Milutinovic, Completeness of the Lipscomb universal space, Glas. Mat. Ser. III 27(47) (1992), 343-364.
   MathSciNet

10. U. Milutinovic, Contributions to the theory of universal spaces, Ph. D. Thesis (in Croatian), University of Zagreb, 1993.

11. U. Milutinovic, Approximation of maps into Lipscomb's space by embeddings, Houston J. Math. 32 (2006), 143-159.
    MathSciNet

12. A. Nagórko, Characterization and topological rigidity of Nöbeling manifolds, Ph. D. Thesis, Warsaw University, 2006,
    http://arxiv.org/abs/math/0602574.

13. W. Olszewski and L. Piantkiewicz, Closed embeddings of completely metrizable spaces into universal spaces, Glas. Mat. Ser. III 27(47) (1992), 175-181.
    MathSciNet

14. J. C. Perry, Lipscomb's universal space is the attractor of an infinite iterated function system, Proc. Amer. Math. Soc. 124 (1996), 2479-2489.
    MathSciNet     CrossRef

15. K. Tsuda, A note on closed embeddings of finite-dimensional metric spaces, Bull. London Math. Soc. 17 (1985), 275-278.
    MathSciNet     CrossRef

16. K. Tsuda, A note on closed embeddings of finite-dimensional metric spaces II, Bull. Polish Acad. Sci. Math. 33 (1985), 541-546.
    MathSciNet

17. A. Wasko, Spaces universal under closed embeddings for finite-dimensional complete metric spaces, Bull. London Math. Soc. 18 (1986), 293-298.
    MathSciNet     CrossRef