Glasnik Matematicki, Vol. 42, No.1 (2007), 69-82.
HOMOTOPY CHARACTERIZATION OF G-ANR'S
Natella Antonyan, Sergey A. Antonyan and Alejandra Soria-Pérez
Departamento de Matemáticas, Division de Ingenieria y Arquitectura,
Instituto Tecnológico y de Estudios Superiores de Monterrey,
Campus Ciudad de México, 14380 México Distrito Federal, México
e-mail: nantonya@itesm.mx
Departamento de Matemáticas, Facultad de Ciencias, Universidad Nacional Autónoma de
México, 04510 México Distrito Federal, México
e-mail: antonyan@servidor.unam.mx
Escuela de Matemáticas, Universidad Juárez del Estado de Durango, 34120 Durango, Dgo.,
México
e-mail: ale_godel@hotmail.com
Abstract. Let G be a compact Lie group. We prove that if each
point x 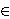 X
of a G-space X admits a Gx-invariant
neighborhood U which is a Gx-ANE
then X is a
G-ANE, where Gx stands for the stabilizer of x. This result
is further applied to give two equivariant homotopy
characterizations of G-ANR's. One of them sounds as follows: a
metrizable G-space Y is a G-ANR iff Y is locally
G-contractible and every metrizable closed G-pair (X, A) has
the G-equivariant homotopy extension property with respect to
Y. In the same terms we also characterize G-ANR subsets of a
given G-ANR space.
X
of a G-space X admits a Gx-invariant
neighborhood U which is a Gx-ANE
then X is a
G-ANE, where Gx stands for the stabilizer of x. This result
is further applied to give two equivariant homotopy
characterizations of G-ANR's. One of them sounds as follows: a
metrizable G-space Y is a G-ANR iff Y is locally
G-contractible and every metrizable closed G-pair (X, A) has
the G-equivariant homotopy extension property with respect to
Y. In the same terms we also characterize G-ANR subsets of a
given G-ANR space.
2000 Mathematics Subject Classification.
54C55, 55P91.
Key words and phrases. G-ANR, G-homotopy, G-homotopy extension
theorem, slice.
Full text (PDF) (free access)
DOI: 10.3336/gm.42.1.05
References:
- S. A. Antonyan,
Retracts in categories of G-spaces,
Izv. Akad. Nauk Armyan. SSR Ser. Mat. 15 (1980), 365-378;
English translation in: Soviet J. Contemporary Math. Anal. 15 (1980), 30-43.
MathSciNet
- S. A. Antonian,
Equivariant embeddings into G-ARs,
Glas. Mat. Ser. III 22(42) (1987), 503-533.
MathSciNet
- S. Antonyan, E. Elfving, and A. Mata-Romero,
Adjunction spaces and unions of G-ANE's,
Topology Proc. 26 (2001/02), 1-28.
MathSciNet
- S. A. Antonyan,
Orbit spaces and unions of equivariant
absolute neighborhood extensors, Topology Appl. 146/147 (2005) 289-315.
MathSciNet
CrossRef
- S. A. Antonyan,
Orbit spaces of proper equivariant absolute extensors,
Topology Appl. 153 (2005), 698-709.
MathSciNet
CrossRef
- K. Borsuk,
Theory of Retracts, PWN-Polish Scientific Publishers, Warszawa, 1967.
MathSciNet
- G. E. Bredon,
Introduction to Compact Transformation Groups,
Academic Press, New York-London, 1972.
MathSciNet
- T. tom Dieck,
Transformation Groups, Walter de Gruyter & Co.,
Berlin, 1987.
MathSciNet
- O. Hanner,
Some theorems on absolute neighborhood retracts,
Ark. Mat. 1 (1951) 389-408.
MathSciNet
CrossRef
- S. T. Hu,
Theory of Retracts, Wayne State University Press,
Detroit, 1965.
MathSciNet
- J. Jaworowski,
Extension properties of G-maps, in:
Proceedings of the International Conference on Geometric Topology
(Warsaw, 1978), PWN, Warsaw, 1980, 209-213.
MathSciNet
- J. van Mill,
Infinite-dimensional Topology. Prerequisites and
Introduction, North Holland Publishing Co., Amsterdam-New
York-Oxford-Tokyo, 1989.
MathSciNet
- R. S. Palais,
The classification of G-spaces, Mem. Amer. Math.
Soc. 36, Providence, 1960.
MathSciNet
- J. de Vries,
Topics in the theory of topological
transformation groups, in: Topological Structures II. Math.
Centre Tracts 116, Math. Centrum, Amsterdam, 1979,
291-304.
MathSciNet
Glasnik Matematicki Home Page
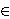 X
X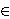 X
X