Glasnik Matematicki, Vol. 41, No.2 (2006), 271-274.
FINITE NONABELIAN 2-GROUPS IN WHICH ANY TWO NONCOMMUTING ELEMENTS GENERATE A
SUBGROUP OF MAXIMAL CLASS
Zvonimir Janko
Mathematical Institute, University of Heidelberg, 69120 Heidelberg, Germany
e-mail: janko@mathi.uni-heidelberg.de
Abstract.
We determine here the structure of the title groups.
It turns out that such a group G
is either quasidihedral or G = HZ(G),
where H is of maximal
class or extraspecial and
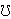
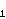 (Z(G)) ≤ Z(H).
This solves a
problem stated by Berkovich. The corresponding problem for p > 2
is open but very difficult since the p-groups of maximal class
are not classified for p > 2.
(Z(G)) ≤ Z(H).
This solves a
problem stated by Berkovich. The corresponding problem for p > 2
is open but very difficult since the p-groups of maximal class
are not classified for p > 2.
2000 Mathematics Subject Classification.
20D15.
Key words and phrases. Finite 2-groups, 2-groups of
maximal class, minimal nonabelian 2-groups, quasidihedral
2-groups, Hughes Hp-subgroups.
Full text (PDF) (free access)
DOI: 10.3336/gm.41.2.09
References:
- Y. Berkovich,
Groups of prime power order, Parts I, II, and III (with Z. Janko), in preparation.
- L. S. Kazarin,
Groups with certain conditions imposed on the normalizers of
subgroups, Perm. Gos. Univ. Ucen. Zap. 218 (1969),
268-279 (Russian).
MathSciNet
- Z. Janko,
Finite 2-groups with small centralizer of an involution,
J. Algebra 241 (2001), 818-826.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
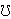
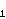 (Z(G)) ≤ Z(H).
(Z(G)) ≤ Z(H).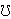
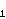 (Z(G)) ≤ Z(H).
(Z(G)) ≤ Z(H).