Glasnik Matematicki, Vol. 41, No.1 (2006), 177-186.
LARGE TIME BEHAVIOR OF DIRICHLET HEAT KERNELS ON
UNBOUNDED DOMAINS ABOVE THE GRAPH OF A BOUNDED LIPSCHITZ FUNCTION
Kittipat Wong
Department of Mathematics, Faculty of Science, Chulalongkorn
University, Bangkok 10330, Thailand
e-mail: kittipat.w@chula.ac.th
Abstract. Let D
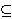 Rd,
d ≥ 2 be the unbounded domain
above the graph of a bounded Lipschitz function. We study the
asymptotic behavior of the transition density
pD(t,x,y) of
killed Brownian motions in D and show that
Rd,
d ≥ 2 be the unbounded domain
above the graph of a bounded Lipschitz function. We study the
asymptotic behavior of the transition density
pD(t,x,y) of
killed Brownian motions in D and show that
limt
→ ∞
t(d+2)/2 pD(t,x,y) =
C1u(x)u(y),
where u is
a minimal harmonic function corresponding to the Martin point at
infinity and C1 is a positive constant.
2000 Mathematics Subject Classification.
60J65, 35J05.
Key words and phrases. Dirichlet heat kernels,
asymptotic behavior, Brownian motions.
Full text (PDF) (free access)
DOI: 10.3336/gm.41.1.15
References:
- D. H. Armitage and S. J. Gardiner,
Classical Potential Theory, Springer Monographs in Mathematics,
Springer-Verlag London, Ltd., London, 2001.
MathSciNet
- P. Collet, S. Martinez and J. San Martin,
Asymptotic behavior of a Brownian motion on exterior
domains,
Probab. Theory Related Fields 116 (2000), 303-316.
MathSciNet
CrossRef
- J. L. Doob,
Classical Potential Theory and its
Probabilistic Counterpart, Springer-Verlag, Berlin, 2001.
MathSciNet
- J. Moser,
A Harnack inequality for parabolic differential
equations,
Comm. Pure Appl. Math. 17 (1964), 101-134.
MathSciNet
CrossRef
- R. G. Pinsky,
Positive Harmonic Functions and
Diffusion, Cambridge Studies in Advanced Mathematics 45,
Cambridge University Press, Cambridge, 1995.
MathSciNet
- S. C. Port and C. J. Stone,
Brownian Motion and
Classical Potential Theory, Academic Press, New York, 1978.
MathSciNet
- N. Trudinger,
Pointwise estimates and
quasilinear parabolic equations,
Comm. Pure Appl. Math. 21 (1968), 205-226.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
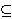 Rd,
Rd,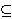 Rd,
Rd,