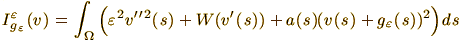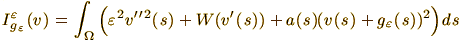Glasnik Matematicki, Vol. 41, No.1 (2006), 89-99.

A NOTE ON CALCULATION OF ASYMPTOTIC ENERGY FOR GINZBURG-LANDAU FUNCTIONAL WITH ε-DEPENDENT 1-LIPSCHITZ PENALIZING TERM IN ONE DIMENSION

Andrija Raguž

Department of Mathematics, University of Zagreb, 10 000 Zagreb, Croatia
e-mail: andrija@math.hr

Abstract.   We study asymptotic behavior of the Ginzburg-Landau functional

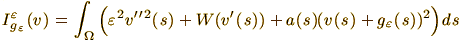
I^{\vep}_{g_{\vep}}(v)=\int_{\Omega}\Big({\vep}^2 v''^2(s)+W(v'(s))+a(s)(v(s)+g_{\vep}(s))^2\Big)ds

as ε → 0, where (gε) is a given sequence of 1-Lipschitz functions. In cases where the sequence (gε) possesses some additional properties we calculate (rescaled) minimal macroscopic energy associated to Iεgε as ε → 0. Thus we obtain partial generalization of our previous results.

2000 Mathematics Subject Classification.   34E15, 49J45.

Key words and phrases.   Young measures, relaxation, Ginzburg-Landau functional, Gamma convergence.

Full text (PDF) (free access)

DOI: 10.3336/gm.41.1.09

References:

  1. G. Alberti and S. Müller, A new approach to variational problems with multiple scales, Comm. Pure Appl. Math. 54 (2001), 761-825.
    MathSciNet     CrossRef

  2. J. M. Ball, A version of the fundamental theorem for Young measures, PDE's and Continuum Models of Phase Transitions, Lecture Notes in Physics 344, Springer, Berlin, 1989, 207-215.
    MathSciNet

  3. R. Choksi, Scaling laws in microphase separation of diblock copolymers, J.Nonlinear Sci. 11 (2001), 223-236.
    MathSciNet

  4. G. Dal Maso, An Introduction to Γ-convergence, Progress in Nonlinear Differential Equations, Birkhäuser, Boston, 1993.
    MathSciNet

  5. A. DeSimone, R. V. Kohn, S. Müller and F. Otto, Magnetic microstructures - a paradigm of multiscale problems, ICIAM 99, Oxford Univ. Press (2000), 175-190.
    MathSciNet

  6. L. C. Evans and R. F. Gariepy, Measure theory and fine properties of functions, CRC Press, Boca Raton, 1992.
    MathSciNet

  7. L. Modica and S. Mortola, Un esempio di Γ-convergenza, Boll. Un. Mat. Ital. B (5) 14 (1977), 285-299.
    MathSciNet

  8. S. Müller, Singular perturbations as a selection criterion for periodic minimizing sequences, Calc. Var. Partial Differential Equations 1 (1993), 169-204.
    MathSciNet

  9. S. Müller, Private communication.

  10. A. Raguz, Relaxation of Ginzburg-Landau functional with 1-Lipschitz penalizing term in one dimension by Young measures on micro-patterns, Asymptotic Anal. 41 (2005), 331-361.
    MathSciNet

  11. A. Raguz, A note on calculation of asymptotic energy for Ginzburg-Landau functional with externally imposed lower-order oscillatory term in one dimension, submitted.

  12. L. Tartar, Beyond Young measures, Meccanica 30 (1995), 505-526.
    MathSciNet     CrossRef

  13. L. C. Young, Lectures on the calculus of variations and optimal control theory, Chelsea Publishing Company, New York, 1980.
Glasnik Matematicki Home Page