Glasnik Matematicki, Vol. 41, No.1 (2006), 57-64.
ON COMMUTATIVITY OF σ-PRIME RINGS
L. Oukhtite and S. Salhi
Université Moulay Ismaïl, Faculté des Sciences et
Techniques, Département de Mathématiques,
B. P. 509-Boutalamine, Errachidia, Maroc
e-mail: oukhtite@math.net
Université Sidi Mohamed Ben Abdellah, Faculté des
Sciences, Département de Mathématiques et Informatique,
B. P. 1796-Atlas, Fes, Maroc
e-mail: salhi@math.net
Abstract. Let R be a 2-torsion free σ-prime ring having a
σ-square closed Lie ideal U and an automorphism T
centralizing on U. We prove that if there exists u0 in
Saσ(R) with
Ru0 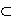 U and if T commutes with
σ on U, then U is contained in the center of R. This
result is then applied to generalize the result of J. Mayne for
centralizing automorphisms to σ-prime rings. Finally, for a
2-torsion free σ-prime ring possessing a nonzero
derivation, we give suitable conditions under which the ring must
be commutative.
U and if T commutes with
σ on U, then U is contained in the center of R. This
result is then applied to generalize the result of J. Mayne for
centralizing automorphisms to σ-prime rings. Finally, for a
2-torsion free σ-prime ring possessing a nonzero
derivation, we give suitable conditions under which the ring must
be commutative.
2000 Mathematics Subject Classification.
16W10, 16W25, 16W20, 16U80.
Key words and phrases. Rings with
involution, σ-prime rings, centralizing automorphisms,
square closed Lie ideals, derivations, commutativity.
Full text (PDF) (free access)
DOI: 10.3336/gm.41.1.05
References:
- R. Awtar,
Lie and Jordan structure in prime rings with derivations,
Proc. Amer. Math. Soc. 41 (1973), 67-74.
MathSciNet
CrossRef
- J. Mayne,
Centralizing automorphisms of prime rings,
Canad. Math. Bull. 19 (1976), 113-115.
MathSciNet
- J. Mayne,
Centralizing mappings of prime rings,
Canad. Math. Bull. 27 (1984), 122-126.
MathSciNet
- J. Mayne,
Centralizing automorphisms of Lie ideals in prime rings,
Canad. Math. Bull. 35 (1992), 510-514.
MathSciNet
- L. Oukhtite and S. Salhi,
σ-prime rings with a special kind of automorphism,
submitted.
- E. C. Posner,
Derivations in prime rings,
Proc. Amer. Math. Soc. 8 (1957), 1093-1100.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
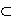 U
U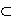 U
U