Glasnik Matematicki, Vol. 41, No.1 (2006), 51-55.
ON FUNCTIONAL EQUATIONS RELATED TO BICIRCULAR PROJECTIONS
Joso Vukman
Department of Mathematics, University of Maribor, PEF, Koroška 160, 2000 Maribor, Slovenia
e-mail: joso.vukman@uni-mb.si
Abstract. In this paper we prove the following result. Let R
be a 2-torsion free semiprime *-ring. Suppose that
D, G : R → R
are additive mappings satisfying the relations
D(xyx) = D(x)yx + xG(y*)*x +
xyD(x),
G(xyx) = G(x)yx + xD(y*)*x
+ xyG(x),
for all pairs x, y 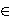 R.
In this case D and G
are of the form
R.
In this case D and G
are of the form
8D(x) = 2(d(x) + g(x)) +
(p + q)x + x(p + q),
8G(x) = 2(d(x) - g(x)) +
(q - p)x + x(q - p),
for all x 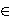 R, where d, g
are derivations of R and p, q are some elements from
symmetric Martindale ring of quotients of R.
Besides, d(x) = -d(x*)*,
g(x) = g(x*)*,
for all x
R, where d, g
are derivations of R and p, q are some elements from
symmetric Martindale ring of quotients of R.
Besides, d(x) = -d(x*)*,
g(x) = g(x*)*,
for all x 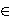 R, and p* = p,
q* = -q.
R, and p* = p,
q* = -q.
2000 Mathematics Subject Classification.
16E99.
Key words and phrases. *-ring, semiprime ring, derivation,
left (right) centralizer, bicircular projection.
Full text (PDF) (free access)
DOI: 10.3336/gm.41.1.04
References:
- K. I. Beidar, W. S. Martindale III and A. V. Mikhalev,
Rings with generalized identities, Marcel Dekker Inc., New York, 1996.
MathSciNet
- M. Bresar,
Jordan mappings of semiprime rings,
J. Algebra 127 (1989), 218-228.
MathSciNet
CrossRef
- M. Fosner and D. Ilisevic,
On a class of projections on *-rings,
Comm. Algebra 33 (2005), 3293-3310.
MathSciNet
- L. L. Stachó and B. Zalar,
Bicircular projections on some
matrix and operator spaces,
Linear Algebra Appl. 384 (2004), 9-20.
MathSciNet
CrossRef
- L. L. Stachó and B. Zalar,
Bicircular projections and
characterization of Hilbert spaces,
Proc. Amer. Math. Soc. 132 (2004), 3019-3025.
MathSciNet
CrossRef
- J. Vukman, I. Kosi-Ulbl and D. Eremita,
On certain equations in rings,
Bull. Austral. Math. Soc. 71 (2005), 53-60.
MathSciNet
Glasnik Matematicki Home Page
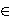 R.
R.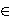 R.
R.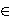 R,
R,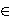 R,
R,