Glasnik Matematicki, Vol. 41, No.1 (2006), 9-30.
ON A CERTAIN FAMILY OF QUARTIC EQUATIONS WITH THREE PARAMETERS
Volker Ziegler
Institut für Mathematik A, Technische Universität Graz, Steyrergasse 30,
A-8010 Graz, Austria
e-mail: ziegler@finanz.math.tugraz.at
Abstract. We consider the parameterized Thue equation
X4 - 4sX3Y -
(2ab + 4(a + b)s)X2Y2
- 4absXY3 + a2b2Y4
= ± 1,
with a, b 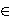 1/4 Z such that
ab
1/4 Z such that
ab 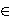 Z. By the
hypergeometric method and a method of Tzanakis we find all
solutions, if s is large with respect to |a| and |b|.
Z. By the
hypergeometric method and a method of Tzanakis we find all
solutions, if s is large with respect to |a| and |b|.
2000 Mathematics Subject Classification.
11D59, 11D25, 11D09.
Key words and phrases. Diophantine equations, parameterized Thue equations, norm form equations, simultaneous
Pellian equations.
Full text (PDF) (free access)
DOI: 10.3336/gm.41.1.02
References:
- A. Baker,
Linear forms in the logarithms of algebraic numbers I, II, III,
Mathematika 13 (1966), 204-216; ibid. 14 (1967), 102-107;
ibid. 14 (1967), 220-228.
MathSciNet
- A. Baker,
Contributions to the theory of Diophantine equations I. On the
representation of integers by binary forms,
Philos. Trans. Roy. Soc. London Ser. A 263 (1967/1968), 173-191.
MathSciNet
- A. Baker,
Linear forms in the logarithms of algebraic numbers IV,
Mathematika 15 (1968), 204-216.
MathSciNet
- A. Baker and H. Davenport,
The equations x2-2=y2 and
8x2-7=z2,
Quart. J. Math. Oxford Ser. (2) 20 (1969), 129-137.
MathSciNet
- M. A. Bennett,
On the number of solutions of simultaneous Pell equations,
J. Reine Angew. Math. 498 (1998), 173-199.
MathSciNet
CrossRef
- Yu. Bilu and G. Hanrot,
Solving Thue equations of high degree,
J. Number Theory 60 (1996), 373-392.
MathSciNet
CrossRef
- Y. Bugeaud and K. Györy,
Bounds for the solutions of Thue-Mahler equations and norm form equations,
Acta Arith. 74 (1996), 273-292.
MathSciNet
- G. V. Chudnovsky,
On the method of Thue-Siegel,
Ann. of Math. (2) 117 (1983), 325-382.
MathSciNet
- A. Dujella and B. Jadrijevic,
A parametric family of quartic Thue equations,
Acta Arith. 101 (2002), 159-170.
MathSciNet
- A. Dujella and B. Jadrijevic,
A family of quartic Thue inequalities,
Acta Arith. 111 (2004), 61-76.
MathSciNet
- S. Lang,
Algebra, Springer-Verlag, New York, 2002.
MathSciNet
- K. Mahler,
Zur Approximation algebraischer Zahlen (I),
Math. Ann. 107 (1933), 691-730.
MathSciNet
CrossRef
- L. J. Mordell,
Diophantine equations, Academic Press, London, 1969.
MathSciNet
- E. Thomas,
Complete solutions to a family of cubic Diophantine
equations,
J. Number Theory 34 (1990), 235-250.
MathSciNet
CrossRef
- A. Thue,
Über Annäherungswerte algebraischer Zahlen,
J. Reine und Angew. Math. 135 (1909), 284-305.
Jahrbuch
- A. Thue,
Berechnung aller Lösungen gewisser Gleichungen von der Form
axr - byr = f,
Vid. Skrivter I Mat.- Naturv. Klasse 4 (1918), 1-9.
Jahrbuch
- N. Tzanakis,
Explicit solution of a class of quartic Thue equations,
Acta Arith. 64 (1993), 271-283.
MathSciNet
- N. Tzanakis and B. M. M. de Weger,
On the practical solution of the Thue equation,
J. Number Theory 31 (1989), 99-132.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
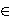 1/4 Z
1/4 Z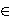 1/4 Z
1/4 Z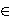 Z.
Z.