Glasnik Matematicki, Vol. 41, No.1 (2006), 1-8.
COMPUTATIONAL EXPERIENCES ON NORM FORM EQUATIONS FORMING ARITHMETIC PROGRESSIONS
A. Bérczes and A. Pethö
Institute of Mathematics, University of Debrecen,
Number Theory Research Group, Hungarian Academy of Sciences and
University of Debrecen, H-4010 Debrecen, P.O. Box 12,
Hungary
e-mail: berczesa@math.klte.hu
Faculty of Informatics, University of Debrecen,
H-4010 Debrecen, P.O. Box 12,
Hungary
e-mail: pethoe@inf.unideb.hu
Abstract. In the present paper we solve the equation
NK/Q(x0 + x1α +
x2α2 + ... +
xn -1αn -1) = 1
in x0, ... , xn -1
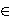 Z,
such that x0, ... , xn -1
is an arithmetic progression, where α is a root of
the polynomial xn - a,
for all integers 2 ≤ a ≤ 100 and
n ≥ 3.
Z,
such that x0, ... , xn -1
is an arithmetic progression, where α is a root of
the polynomial xn - a,
for all integers 2 ≤ a ≤ 100 and
n ≥ 3.
2000 Mathematics Subject Classification.
11D57, 11D59, 11B25.
Key words and phrases. Norm form
equation, arithmetic progression, binomial Thue equation.
Full text (PDF) (free access)
DOI: 10.3336/gm.41.1.01
References:
- M. A. Bennett,
Rational approximation to algebraic
numbers of small height: the Diophantine equation
| axn - byn | =1,
J. Reine Angew. Math. 535 (2001), 1-49.
MathSciNet
CrossRef
- M. A. Bennett,
Products of consecutive integers,
Bull. London Math. Soc. 36 (2004), 683-694.
MathSciNet
CrossRef
- M. A. Bennett, K. Györy and Á. Pintér,
On the Diophantine equation
1k + 2k + ... + xk =
yn,
Compos. Math. 140 (2004), 1417-1431.
MathSciNet
- M. A. Bennett and C. M. Skinner,
Ternary Diophantine equations via Galois representations and modular forms,
Canad. J. Math. 56 (2004), 23-54.
MathSciNet
- M. A. Bennett, V. Vatsal and S. Yazdani,
Ternary Diophantine equations of signature (p,p,3),
Compos. Math. 140 (2004), 399-1416.
2098394">MathSciNet
- A. Bérczes and A. Pethö,
On norm form equations with solutions forming arithmetic progressions,
Publ. Math. Debrecen 65 (2004), 281-290.
MathSciNet
- Yu. Bilu, G. Hanrot and P. M. Voutier,
Existence of primitive divisors of Lucas and Lehmer numbers,
J. Reine Angew. Math. 539 (2001), 75-122.
MathSciNet
CrossRef
- W. Bosma, J. Cannon and C. Playoust,
The Magma algebra system. I. The user language,
J. Symbolic Comput. 24 (1997), 235-265.
MathSciNet
CrossRef
- J. Buchmann and A. Pethö,
Computation of independent units in number fields by Dirichlet's method,
Math. Comp. 52 (1989), 149-159, S1-S14.
MathSciNet
- H. Darmon and L. Merel,
Winding quotients and some variants of Fermat's last theorem,
J. Reine Angew. Math. 490 (1997), 81-100.
MathSciNet
- K. Györy, I. Pink and Á. Pintér,
Power values of polynomials and binomial Thue-Mahler equations,
Publ. Math. Debrecen 65 (2004), 341-362.
MathSciNet
- K. Györy and Á. Pintér,
Almost perfect powers in products of consecutive integers,
Monatsh. Math. 145 (2005), 19-33.
MathSciNet
CrossRef
- G.Hanrot,
Solving Thue equations without the full
unit group, Math. Comp. 69 (2000), 395-405.
MathSciNet
CrossRef
- G. Hanrot, N. Saradha and T. N. Shorey,
Almost perfect powers in consecutive integers,
Acta Arith. 99 (2001), 13-25.
MathSciNet
- A. Kraus,
Majorations effectives pour l'équation de
Fermat généralisée,
Canad. J. Math. 49 (1997), 1139-1161.
MathSciNet
- M. Mignotte,
A note on the equation
axn - byn = c,
Acta Arith. 75 (1996), 287-295.
MathSciNet
- L. J. Mordell,
Diophantine equations, Academic Press, London, 1969.
MathSciNet
- Á. Pintér,
On the power values of power sums,
J. Number Theory, to appear.
- K. A. Ribet,
On the equation ap + 2α
bp + cp = 0,
Acta Arith. 79 (1997), 7-16.
MathSciNet
- J.-P. Serre,
Sur les représentations modulaires de
degré 2 de
Gal(Q/Q),
Duke Math. J. 54 1987), 179-230.
MathSciNet
CrossRef
- T. N. Shorey and R. Tijdeman,
Exponential Diophantine equations, Cambridge Univ. Press, Cambridge-New York, 1986.
MathSciNet
- S. Siksek and J. E. Cremona,
On the Diophantine equation x2+7=ym,
Acta Arith. 109 (2003), 143-149.
MathSciNet
- W. Stein,
The Modular Forms Database,
http://modular.ucsd.edu/Tables
(2004).
- The PARIGroup, Bordeaux, PARI/GP, version 2.1.5,
2004,
available from
http://pari.math.u-bordeaux.fr/.
- A. Wiles,
Modular elliptic curves and Fermat's last
theorem, Ann. of Math. (2) 141 (1995), 443-551.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
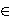 Z,
Z,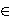 Z,
Z,