Glasnik Matematicki, Vol. 40, No.2 (2005), 339-345.
A LOCAL TO GLOBAL SELECTION THEOREM FOR SIMPLEX-VALUED FUNCTIONS
Ivan Ivanšić and Leonard R. Rubin
Department of Mathematics, University of Zagreb,
Unska 3, P.O. Box 148, 10001 Zagreb, Croatia
e-mail: ivan.ivansic@fer.hr
Department of Mathematics, University of Oklahoma,
Norman, Oklahoma 73019, USA
e-mail: lrubin@ou.edu
Abstract. Suppose we are given a function
σ : X
→ K
where X is a
paracompact space and K is a simplicial complex, and an open
cover
{Uα |
α 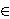 Γ}
of X,
so that for each
α
Γ}
of X,
so that for each
α 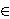 Γ,
fα :
Uα →
|K|
is a map that is a
selection of
σ
on its domain. We shall prove that there is
a map
f : X → |K|
which is a selection of
σ. We shall also
show that under certain conditions on such a set of maps or on the
complex K, there exists a
σ : X
→ K
with the property that
each
fα
is a selection of
σ
on its domain and that
there is a selection
f : X →
|K| of σ. The term selection,
as used herein, will always refer to a map f, i.e., continuous
function, having the property that
f(x)
Γ,
fα :
Uα →
|K|
is a map that is a
selection of
σ
on its domain. We shall prove that there is
a map
f : X → |K|
which is a selection of
σ. We shall also
show that under certain conditions on such a set of maps or on the
complex K, there exists a
σ : X
→ K
with the property that
each
fα
is a selection of
σ
on its domain and that
there is a selection
f : X →
|K| of σ. The term selection,
as used herein, will always refer to a map f, i.e., continuous
function, having the property that
f(x)
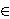 σ(x)
for each x in the domain.
σ(x)
for each x in the domain.
2000 Mathematics Subject Classification.
54C65, 54C05, 54E20.
Key words and phrases. Contiguous functions, continuous function, discrete
collection, infinite simplex, K-modification, locally
finite-dimensional complex, paracompact, polyhedron, principal
simplex, selection, simplex, simplicial complex.
Full text (PDF) (free access)
DOI: 10.3336/gm.40.2.14
References:
- R. Engelking,
General Topology, PWN-Polish Scientific Publishers, Warsaw, 1977.
- I. Ivansic and L. Rubin,
A selection theorem
for simplex-valued maps,
Glas. Mat. Ser. III 39(59) (2004), 331-333.
- S. Mardesic,
Extension dimension of inverse limits,
Glas. Mat. Ser. III 35(55) (2000), 339-354.
- S. Mardesic,
Extension dimension of inverse limits.
Correction of a proof.,
Glas. Mat. Ser. III 39(59) (2004), 335-337.
- E. Michael,
Local properties of topological spaces,
Duke Mat. J. 21 (1954), 163-171.
CrossRef
- L. Rubin,
Relative collaring,
Proc. Amer. Math. Soc. 55 (1976), 181-184.
CrossRef
Glasnik Matematicki Home Page
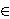 Γ}
Γ}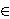 Γ,
Γ, 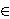 σ(x)
σ(x) 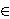 Γ}
Γ}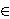 Γ,
Γ, 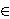 σ(x)
σ(x)