Glasnik Matematicki, Vol. 40, No.1 (2005), 51-58.
A PROPERTY OF GROUPS OF ORDER
≤ pp(e+1) AND EXPONENT pe
Yakov Berkovich
Department of Mathematics, University of Haifa,
Haifa 31905, Israel
e-mail: berkov@mathcs2.haifa.ac.il
Abstract. Let G be a p-group of exponent
pe and order
pm,
where m < p(e+1)
if p > 2 and m
≤ 2(e+1) if
p = 2. Then, if
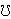 e-1(G) is irregular,
then p = 2, e = 2 and
e-1(G) is irregular,
then p = 2, e = 2 and
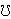 e-1(G)
e-1(G)
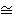 D8 × C2, where
|C2| = 2 and D8 is dihedral of order 8.
D8 × C2, where
|C2| = 2 and D8 is dihedral of order 8.
2000 Mathematics Subject Classification.
20C15.
Key words and phrases. Pyramidal, regular, absolutely
regular, irregular and metacyclic p-groups,
p-groups of maximal class.
Full text (PDF) (free access)
DOI: 10.3336/gm.40.1.06
References:
- Y. Berkovich,
Groups of Prime Power Order, Part I, in preparation.
- Y. Berkovich,
On subgroups and epimorphic images of finite p-groups,
J. Algebra 248 (2002), 472-553.
- Y. Berkovich,
Some consequences of Maschke's theorem,
Algebra Coll. 5 (1998), 143-158.
- Y. Berkovich,
On subgroups of finite p-groups,
J. Algebra 224 (2000), 198-240.
CrossRef
- Z. Janko, private communication.
- A. Mann,
The power structure of p-groups,
J. Algebra 42 (1976), 121-135.
CrossRef
- M. Suzuki,
Group Theory II, Springer, New York, 1986.
- B. Wilkens,
On the upper exponent of a finite p-group,
J. Algebra 277 (2004), 349-363.
CrossRef
Glasnik Matematicki Home Page
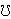 e-1(G)
e-1(G)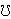 e-1(G)
e-1(G)
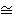 D8 × C2,
D8 × C2,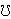 e-1(G)
e-1(G)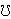 e-1(G)
e-1(G)
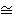 D8 × C2,
D8 × C2,